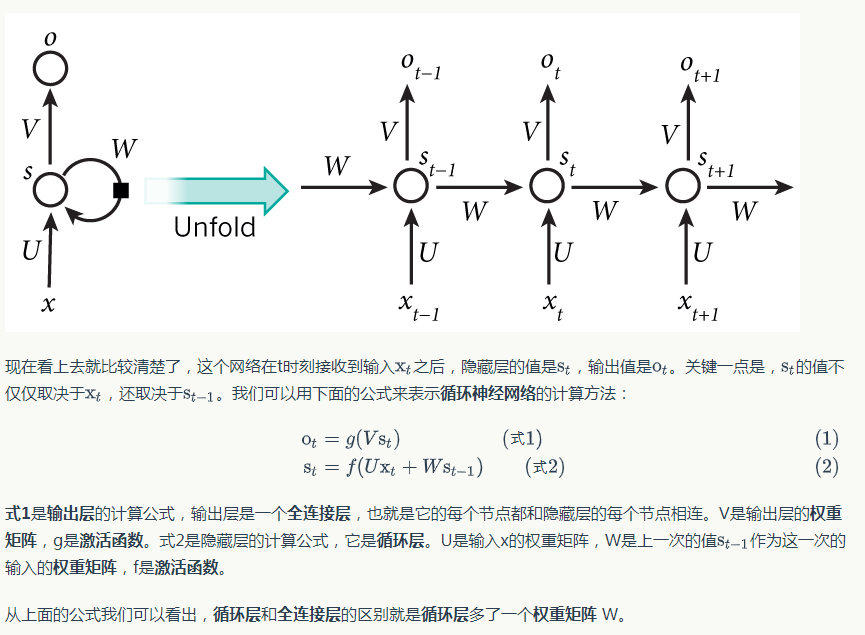
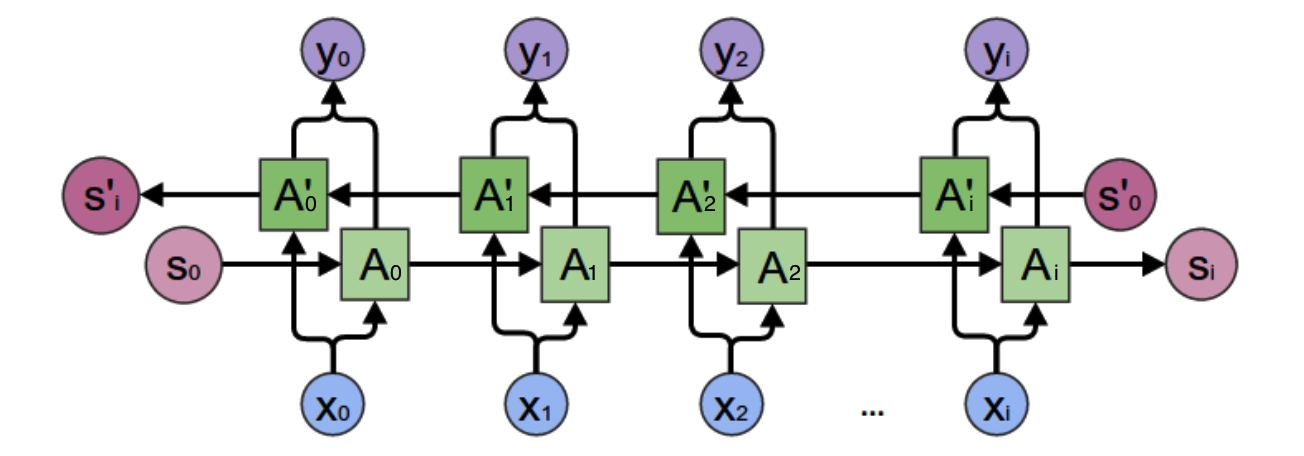
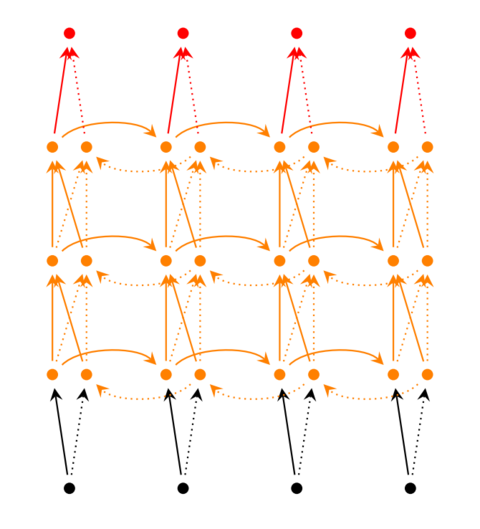
RNN公式解析:
双向循环神经网络:
计算方式:
前面我们介绍的循环神经网络只有一个隐藏层,我们当然也可以堆叠两个以上的隐藏层,这样就得到了深度循环神经网络
权重更新部分采用的是BPTT训练算法,详情参见:
https://zybuluo.com/hanbingtao/note/541458
RNN简单代码实现:
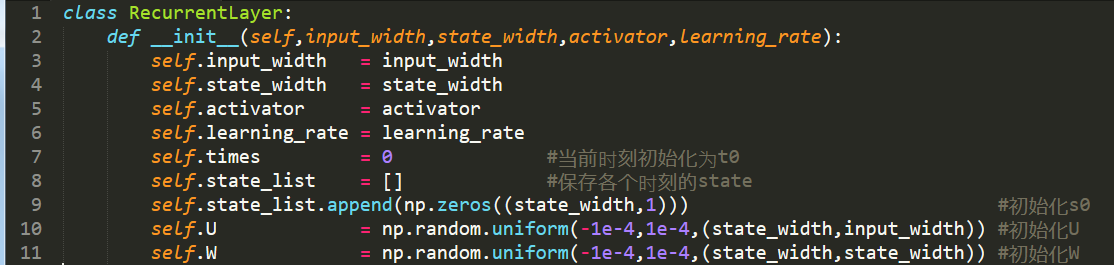
1.用RecurrentLayer类来实现一个循环层,初始化一个循环层,可以在构造函数中设置循环层的超参数,循环层有两个权重数组,U和W:
2.在forward方法中,实现循环层的前向计算
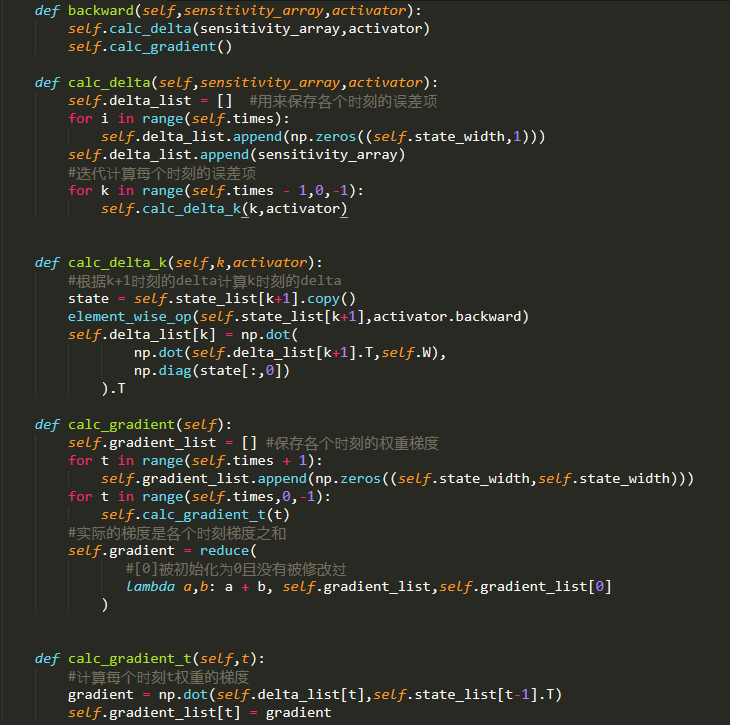
3.在backword方法中,实现BPTT算法。
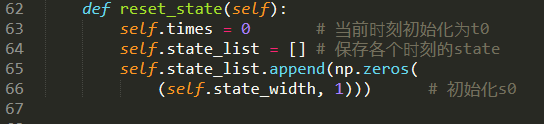
4.循环层是一个带状态的层,每次forword都会改变循环层的内部状态,这给梯度检查带来了麻烦。因此,我们需要一个reset_state方法,来重置循环层的内部状态。
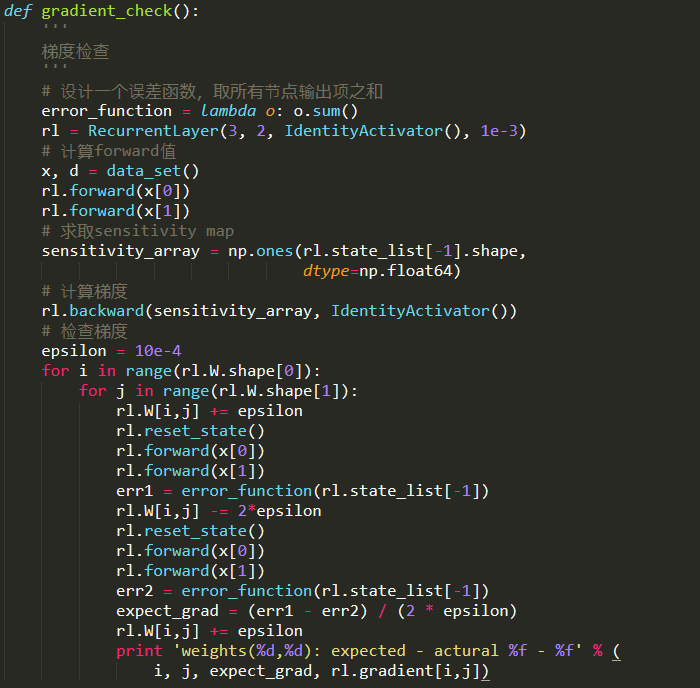
5.梯度检查的代码。
需要注意,每次计算error之前,都要调用reset_state方法重置循环层的内部状态
完整代码:
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
import numpy as np
from activators import ReluActivator, IdentityActivator
# 对numpy数组进行element wise操作
def element_wise_op(array, op):
for i in np.nditer(array,op_flags=['readwrite']):
i[...] = op(i)
class RecurrentLayer:
def __init__(self, input_width, state_width,
activator, learning_rate):
self.input_width = input_width
self.state_width = state_width
self.activator = activator
self.learning_rate = learning_rate
self.times = 0 # 当前时刻初始化为t0
self.state_list = [] # 保存各个时刻的state
self.state_list.append(np.zeros(
(state_width, 1))) # 初始化s0
self.U = np.random.uniform(-1e-4, 1e-4,
(state_width, input_width)) # 初始化U
self.W = np.random.uniform(-1e-4, 1e-4,
(state_width, state_width)) # 初始化W
def forward(self, input_array):
'''
根据『式2』进行前向计算
'''
self.times += 1
state = (np.dot(self.U, input_array) +
np.dot(self.W, self.state_list[-1]))
element_wise_op(state, self.activator.forward)
self.state_list.append(state)
def backward(self, sensitivity_array,
activator):
'''
实现BPTT算法
'''
self.calc_delta(sensitivity_array, activator)
self.calc_gradient()
def update(self):
'''
按照梯度下降,更新权重
'''
self.W -= self.learning_rate * self.gradient
def calc_delta(self, sensitivity_array, activator):
self.delta_list = [] # 用来保存各个时刻的误差项
for i in range(self.times):
self.delta_list.append(np.zeros(
(self.state_width, 1)))
self.delta_list.append(sensitivity_array)
# 迭代计算每个时刻的误差项
for k in range(self.times - 1, 0, -1):
self.calc_delta_k(k, activator)
def calc_delta_k(self, k, activator):
'''
根据k+1时刻的delta计算k时刻的delta
'''
state = self.state_list[k+1].copy()
element_wise_op(self.state_list[k+1],
activator.backward)
self.delta_list[k] = np.dot(
np.dot(self.delta_list[k+1].T, self.W),
np.diag(state[:,0])).T
def calc_gradient(self):
self.gradient_list = [] # 保存各个时刻的权重梯度
for t in range(self.times + 1):
self.gradient_list.append(np.zeros(
(self.state_width, self.state_width)))
for t in range(self.times, 0, -1):
self.calc_gradient_t(t)
# 实际的梯度是各个时刻梯度之和
self.gradient = reduce(
lambda a, b: a + b, self.gradient_list,
self.gradient_list[0]) # [0]被初始化为0且没有被修改过
def calc_gradient_t(self, t):
'''
计算每个时刻t权重的梯度
'''
gradient = np.dot(self.delta_list[t],
self.state_list[t-1].T)
self.gradient_list[t] = gradient
def reset_state(self):
self.times = 0 # 当前时刻初始化为t0
self.state_list = [] # 保存各个时刻的state
self.state_list.append(np.zeros(
(self.state_width, 1))) # 初始化s0
def data_set():
x = [np.array([[1], [2], [3]]),
np.array([[2], [3], [4]])]
d = np.array([[1], [2]])
return x, d
def gradient_check():
'''
梯度检查
'''
# 设计一个误差函数,取所有节点输出项之和
error_function = lambda o: o.sum()
rl = RecurrentLayer(3, 2, IdentityActivator(), 1e-3)
# 计算forward值
x, d = data_set()
rl.forward(x[0])
rl.forward(x[1])
# 求取sensitivity map
sensitivity_array = np.ones(rl.state_list[-1].shape,
dtype=np.float64)
# 计算梯度
rl.backward(sensitivity_array, IdentityActivator())
# 检查梯度
epsilon = 10e-4
for i in range(rl.W.shape[0]):
for j in range(rl.W.shape[1]):
rl.W[i,j] += epsilon
rl.reset_state()
rl.forward(x[0])
rl.forward(x[1])
err1 = error_function(rl.state_list[-1])
rl.W[i,j] -= 2*epsilon
rl.reset_state()
rl.forward(x[0])
rl.forward(x[1])
err2 = error_function(rl.state_list[-1])
expect_grad = (err1 - err2) / (2 * epsilon)
rl.W[i,j] += epsilon
print ('weights(%d,%d): expected - actural %f - %f' % (
i, j, expect_grad, rl.gradient[i,j]))
def test():
l = RecurrentLayer(3, 2, ReluActivator(), 1e-3)
x, d = data_set()
l.forward(x[0])
l.forward(x[1])
l.backward(d, ReluActivator())
return l
关于BPTT算法的另外一种实现:
class RNN2(RNN1):
# 定义 Sigmoid 激活函数
def activate(self, x):
return 1 / (1 + np.exp(-x))
# 定义 Softmax 变换函数
def transform(self, x):
safe_exp = np.exp(x - np.max(x))
return safe_exp / np.sum(safe_exp)
def bptt(self, x, y):
x, y, n = np.asarray(x), np.asarray(y), len(y)
# 获得各个输出,同时计算好各个 State
o = self.run(x)
# 照着公式敲即可 ( σ'ω')σ
dis = o - y
dv = dis.T.dot(self._states[:-1])
du = np.zeros_like(self._u)
dw = np.zeros_like(self._w)
for t in range(n-1, -1, -1):
st = self._states[t]
ds = self._v.T.dot(dis[t]) * st * (1 - st)
# 这里额外设定了最多往回看 10 步
for bptt_step in range(t, max(-1, t-10), -1):
du += np.outer(ds, x[bptt_step])
dw += np.outer(ds, self._states[bptt_step-1])
st = self._states[bptt_step-1]
ds = self._w.T.dot(ds) * st * (1 - st)
return du, dv, dw
def loss(self, x, y):
o = self.run(x)
return np.sum(
-y * np.log(np.maximum(o, 1e-12)) -
(1 - y) * np.log(np.maximum(1 - o, 1e-12))
)
注意我们设定了在每次沿时间通道反向传播时、最多往回看 10 步
RNN-Tensorflow实例
实例1:
from __future__ import print_function
import tensorflow as tf
from tensorflow.contrib import rnn
# Import MNIST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
'''
To classify images using a recurrent neural network, we consider every image
row as a sequence of pixels. Because MNIST image shape is 28*28px, we will then
handle 28 sequences of 28 steps for every sample.
'''
# Training Parameters
learning_rate = 0.001
training_steps = 10000
batch_size = 128
display_step = 200
# Network Parameters
num_input = 28 # MNIST data input (img shape: 28*28)
timesteps = 28 # timesteps
num_hidden = 128 # hidden layer num of features
num_classes = 10 # MNIST total classes (0-9 digits)
# tf Graph input
X = tf.placeholder("float", [None, timesteps, num_input])
Y = tf.placeholder("float", [None, num_classes])
# Define weights
weights = {
'out': tf.Variable(tf.random_normal([num_hidden, num_classes]))
}
biases = {
'out': tf.Variable(tf.random_normal([num_classes]))
}
def RNN(x, weights, biases):
# Prepare data shape to match `rnn` function requirements
# Current data input shape: (batch_size, timesteps, n_input)
# Required shape: 'timesteps' tensors list of shape (batch_size, n_input)
# Unstack to get a list of 'timesteps' tensors of shape (batch_size, n_input)
x = tf.unstack(x, timesteps, 1)
# Define a lstm cell with tensorflow
lstm_cell = rnn.BasicLSTMCell(num_hidden, forget_bias=1.0)
# Get lstm cell output
outputs, states = rnn.static_rnn(lstm_cell, x, dtype=tf.float32)
# Linear activation, using rnn inner loop last output
return tf.matmul(outputs[-1], weights['out']) + biases['out']
logits = RNN(X, weights, biases)
prediction = tf.nn.softmax(logits)
# Define loss and optimizer
loss_op = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
logits=logits, labels=Y))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
train_op = optimizer.minimize(loss_op)
# Evaluate model (with test logits, for dropout to be disabled)
correct_pred = tf.equal(tf.argmax(prediction, 1), tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
# Initialize the variables (i.e. assign their default value)
init = tf.global_variables_initializer()
# Start training
with tf.Session() as sess:
# Run the initializer
sess.run(init)
for step in range(1, training_steps+1):
batch_x, batch_y = mnist.train.next_batch(batch_size)
# Reshape data to get 28 seq of 28 elements
batch_x = batch_x.reshape((batch_size, timesteps, num_input))
# Run optimization op (backprop)
sess.run(train_op, feed_dict={X: batch_x, Y: batch_y})
if step % display_step == 0 or step == 1:
# Calculate batch loss and accuracy
loss, acc = sess.run([loss_op, accuracy], feed_dict={X: batch_x,Y: batch_y})
print("Step " + str(step) + ", Minibatch Loss= " + \
"{:.4f}".format(loss) + ", Training Accuracy= " + \
"{:.3f}".format(acc))
print("Optimization Finished!")
# Calculate accuracy for 128 mnist test images
test_len = 128
test_data = mnist.test.images[:test_len].reshape((-1, timesteps, num_input))
test_label = mnist.test.labels[:test_len]
print("Testing Accuracy:", sess.run(accuracy, feed_dict={X: test_data, Y: test_label}))
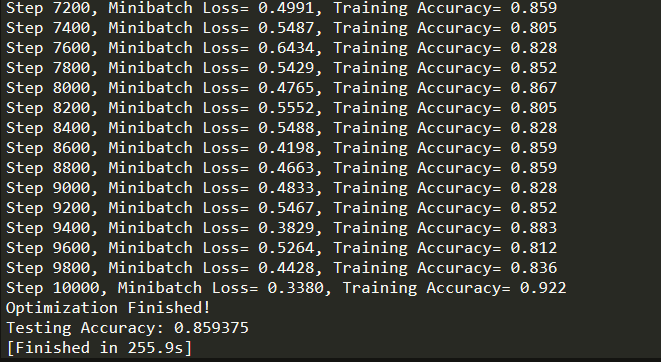
运行结果:
实例2:
from __future__ import print_function
import tensorflow as tf
from tensorflow.contrib import rnn
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/",one_hot = True)
#Training Parameters
learning_rate = 0.001
training_steps = 10000
batch_size = 128
display_step = 200
#Network Parameters
num_input = 28 # MNIST data input (img shape: 28*28)
timesteps = 28
num_hidden = 128
num_classes = 10
#tf Graph input
X = tf.placeholder("float",[None,timesteps,num_input])
Y = tf.placeholder("float",[None,num_classes])
#Define weights and biases
weights = {
# Hidden layer weights => 2*n_hidden because of forward + backward cells
'out':tf.Variable(tf.random_normal([2 * num_hidden,num_classes]))
}
biases = {
'out':tf.Variable(tf.random_normal([num_classes]))
}
def BiRNN(x,weights,biases):
# Unstack to get a list of 'timesteps' tensors of shape (batch_size, num_input)
x = tf.unstack(x,timesteps,1)
#Define lstm cells with tensorflow
#Forward direction cell
lstm_fw_cell = rnn.BasicLSTMCell(num_hidden, forget_bias = 1.0)
#Backward direction cell
lstm_bw_cell = rnn.BasicLSTMCell(num_hidden, forget_bias = 1.0)
#Get lstm cell output
try:
outputs,_,_ = rnn.static_bidirectional_rnn(lstm_fw_cell,lstm_bw_cell,x,dtype = tf.float32)
except Exception:
# Old TensorFlow version only returns outputs not states
outputs = rnn.static_bidirectional_rnn(lstm_fw_cell,lstm_bw_cell,x,dtype = tf.float32)
#Linear activation, using rnn inner loop last output
return tf.matmul(outputs[-1],weights['out']) + biases['out']
logits = BiRNN(X,weights,biases)
prediction = tf.nn.softmax(logits)
#Define loss and optimizer
loss_op = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = logits, labels = Y))
optimizer = tf.train.GradientDescentOptimizer(learning_rate = learning_rate)
train_op = optimizer.minimize(loss_op)
correct_pred = tf.equal(tf.argmax(prediction,1),tf.argmax(Y,1))
accuracy = tf.reduce_mean(tf.cast(correct_pred,tf.float32))
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
for step in range(1,training_steps + 1):
batch_x,batch_y = mnist.train.next_batch(batch_size)
# Reshape data to get 28 seq of 28 elements
batch_x = batch_x.reshape((batch_size, timesteps, num_input))
# Run optimization op (backprop)
sess.run(train_op, feed_dict={X: batch_x, Y: batch_y})
if step % display_step == 0 or step == 1:
# Calculate batch loss and accuracy
loss, acc = sess.run([loss_op, accuracy], feed_dict={X: batch_x,
Y: batch_y})
print("Step " + str(step) + ", Minibatch Loss= " + \
"{:.4f}".format(loss) + ", Training Accuracy= " + \
"{:.3f}".format(acc))
print("Optimization Finished!")
# Calculate accuracy for 128 mnist test images
test_len = 128
test_data = mnist.test.images[:test_len].reshape((-1, timesteps, num_input))
test_label = mnist.test.labels[:test_len]
print("Testing Accuracy:",sess.run(accuracy, feed_dict={X: test_data, Y: test_label}))
运行结果:
点击查看更多内容
为 TA 点赞
评论
共同学习,写下你的评论
评论加载中...
作者其他优质文章
正在加载中
感谢您的支持,我会继续努力的~
扫码打赏,你说多少就多少
赞赏金额会直接到老师账户
支付方式
打开微信扫一扫,即可进行扫码打赏哦