单纯形法简介在其他网站上都可以查到,我就不多说了
我们主要说方法
它主要解决的是局部最优解的问题
利用多边形进行求解的,若有n个变量,则利用n+1边形
我们这里以两个变量为例,求解第三维度的最优解
例如解决
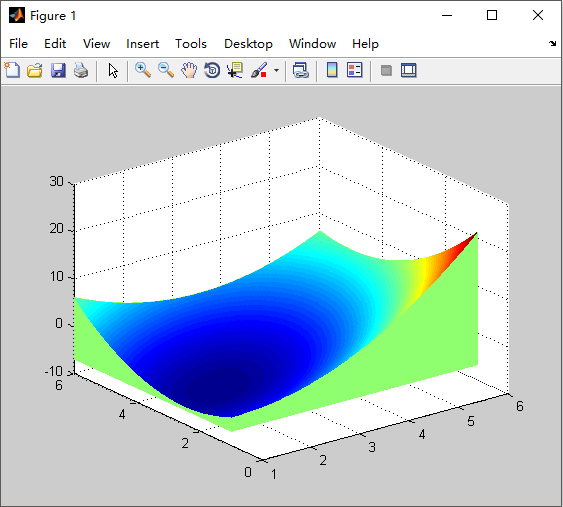
min f(x,y)=x2 - 4*x + y2 - y - x*y
matlab 图
可以看出,差不多是(3,2)附近取得最小
我们来用下山单纯形求解
我们设立三个初始点 (0,0),(1.2,0),(0,0.8)
我们把它们分别带入f中,函数值越小的越接近解,我们把它称为最好点,反之,函数值最大的点,我们称之为最坏点
我们要做的是,利用已知点,寻找更加接近解的点
我们需要了解几种寻找下一个点的思想
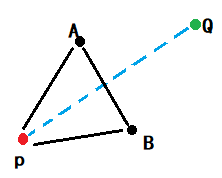
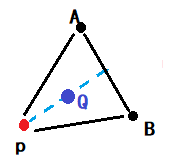
反射 reflect
假设三角形的三个点是ABP,其中P是最坏点,那么我们寻找一个Q点,使得APBQ是一个平行四边形
设向量α为p->A,β为p->B (假设1)
那么Q = p + (α+β),其中p和Q是坐标
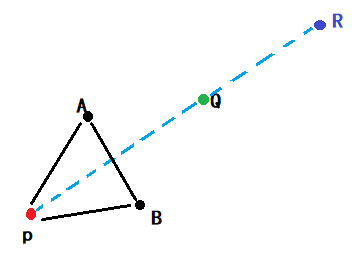
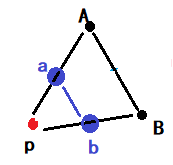
扩张 extern
假设,我们得到的新点Q,它比原来三角形中最好的点还要好,那么,我们可以假定这个探索方向是正确的,我们不妨再往前走一步!
其中Q->R = (p->R)/2,我们这里称扩张Q点
设向量α为Q->A, β为Q->B (假设2)
于是,R = Q - (α+β)/2
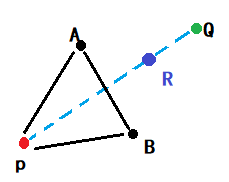
收缩 Shrink
我认为收缩有两种
因为我们一般先做反射点,所以,之后的操作如果针对反射点,那么就是对反射点进行收缩
基于(假设2),R = Q + (α+β)/4
还有一种是最优解本来就在三角形PAB中,我们对P做收缩
基于(假设1),则Q = P + (α+β)/4
压缩 compress
我们认为,如果上述操作均没有找到更好的点来替代最坏点,那么说明之前的三角形是非法的,那么我们进行压缩操作
即,取两边中点与最坏点构成新的三角形
我们用下山单纯形法求解步骤如下:
求出初始点的最坏点,构成三角形
重复下述,直到满足精度
先做一次反射
如果反射点比最好点还要好(更加接近条件:min f(x0,y0))->做一次扩张
如果扩张点比反射点还要好->扩张点代替之前的最坏点,形成新的三角形
反之->反射点代替之前的最坏点
反之,如果反射点比最坏点还要坏->反射点做收缩1
如果收缩点1比最坏点好->收缩点1代替最坏点
反之->最坏点做收缩2
如果收缩点2比最坏点好->收缩点2代替最坏点
反之->三角形做收缩
反之,反射点代替最坏点,形成新的三角形
C++代码:
triangle.h
#pragma once#define stds std::#define VEC2_OUT#include "lvgm\lvgm.h" //本人博客: https://www.cnblogs.com/lv-anchoret/category/1367052.html#include <vector>#include <algorithm>using namespace lvgm;class Mountain
{public:
typedef dvec2 valtype;
typedef double(*_Fun)(const valtype&);
Mountain() { } /*
p: three position coordinates(in ordered or not)
f: the function Ptr
δ: the solution precision */
Mountain(const valtype& p1, const valtype& p2, const valtype& p3, const double δ)
: _δ(δ)
{
_positions.resize(3);
_positions[0] = p1;
_positions[1] = p2;
_positions[2] = p3;
sort();
} static void setF(_Fun f)
{
_f = f;
} void setδ(double delt)
{
_δ = delt;
}public: /*
origion: the bad position
vec1: bad position -> min position
vec2: bad position -> mid position */
valtype reflect(const valtype& origion, const valtype& vec1, const valtype& vec2)
{ return origion + (vec1 + vec2);
} /*
origion: the change position
vec1: change position -> left position
vec2: change position -> right position */
valtype shrink(const valtype& origion, const valtype& vec1, const valtype& vec2)
{ return origion + (vec1 + vec2) / 4;
} /*
origion: the origion position
vec1: origion position -> left position
vec2: origion position -> right position */
void compression(const valtype& origion, const valtype& vec1, const valtype& vec2)
{
_positions[0] = origion + min(vec1, vec2) / 2;
_positions[1] = origion + max(vec1, vec2) / 2;
}
/*
origion: the change position
vec1: change position -> left position
vec2: change position -> right position */
valtype exter(const valtype& origion, const valtype& vec1, const valtype& vec2)
{ return origion - (vec1 + vec2) / 2;
} void go()
{ double delt = (_positions[2] - _positions[0]).normal(); static int i = 0; while (delt > _δ)
{
stds cout << ++i << "次 " << _positions[0] << "\t" << _positions[1] << "\t" << _positions[2] << stds endl;
valtype t = reflect(_positions[2], _positions[1] - _positions[2], _positions[0] - _positions[2]); if (_f(t) < _f(_positions[0]))
{
valtype ex = exter(t, _positions[1] - t, _positions[0] - t); if (_f(ex) < _f(t))
_positions[2] = ex; else
_positions[2] = t;
} else if (_f(t) > _f(_positions[2]))
{
valtype sh = shrink(t, _positions[1] - t, _positions[0] - t); if (_f(sh) < _f(_positions[2])) //反射点收缩
_positions[2] = sh; else //三角内部内缩 {
sh = reflect(sh, _positions[1] - sh, _positions[0] - sh); if (_f(sh) < _f(_positions[2]))
_positions[2] = sh; else //针对原始点内缩,针对反射点收缩,都不管用,那么选择压缩
compression(_positions[2], _positions[1] - _positions[2], _positions[0] - _positions[2]);
}
} else
_positions[2] = t;
sort();
delt = (_positions[2] - _positions[0]).normal();
}
stds cout << "\n最好点为" << _positions[0] << "\t精度为:" << _δ << stds endl << "函数值为:" << _f(_positions[0]) << stds endl << stds endl;
}protected: const valtype& min(const valtype& vec1, const valtype& vec2)
{ return _f(vec1) < _f(vec2) ? vec1 : vec2;
} const valtype& max(const valtype& vec1, const valtype& vec2)
{ return _f(vec1) > _f(vec2) ? vec1 : vec2;
}
friend bool cmp(const valtype& pos1, const valtype& pos2)
{ return Mountain::_f(pos1) < Mountain::_f(pos2);
} void sort()
{
stds sort(_positions.begin(), _positions.end(), cmp);
}
private:
stds vector<valtype> _positions; //min, mid, max or good, mid, bad
double _δ; static _Fun _f;
};
main.cpp
#include "triangle.h"Mountain::_Fun Mountain::_f=[](const Mountain::valtype& v)->double { return 0.; };int main()
{
auto fun = [](const Mountain::valtype& v)->double
{ return v.x()*v.x() - 4 * v.x() + v.y()*v.y() - v.y() - v.x()*v.y();
};
Mountain m(Mountain::valtype(0, 0), Mountain::valtype(1.2, 0), Mountain::valtype(0, 0.8), 0.1);
m.setF(fun);
m.go();
m.setδ(0.01);
m.go();
m.setδ(0.001);
m.go();
m.setδ(0.0001);
m.go();
m.setδ(0.00001);
m.go();
}
结果:
1次 [ 0, 0 ] [ 1.2, 0 ] [ 0, 0.8 ] 2次 [ 1.2, 0 ] [ 1.2, -0.8 ] [ 0, 0 ] 3次 [ 1.2, 0 ] [ 1.2, -0.8 ] [ 2.4, -0.8 ] 4次 [ 1.2, 0 ] [ 0.6, -0.2 ] [ 1.2, -0.8 ] 5次 [ 1.2, 0 ] [ 0.6, 0.6 ] [ 0.6, -0.2 ] 6次 [ 1.5, 1.3 ] [ 1.2, 0 ] [ 0.6, 0.6 ] 7次 [ 2.1, 0.7 ] [ 1.5, 1.3 ] [ 1.2, 0 ] 8次 [ 2.4, 2 ] [ 2.1, 0.7 ] [ 1.5, 1.3 ] 9次 [ 2.4, 2 ] [ 3, 1.4 ] [ 2.1, 0.7 ] 10次 [ 2.4, 2 ] [ 3, 1.4 ] [ 3.3, 2.7 ] 11次 [ 3, 2.2 ] [ 2.4, 2 ] [ 3, 1.4 ] 12次 [ 3, 2.2 ] [ 2.85, 1.75 ] [ 2.4, 2 ] 13次 [ 3, 2.2 ] [ 2.85, 1.75 ] [ 3.45, 1.95 ] 14次 [ 3, 2.2 ] [ 2.85, 1.75 ] [ 2.6625, 1.9875 ] 15次 [ 3, 2.2 ] [ 3.1875, 1.9625 ] [ 2.85, 1.75 ] 16次 [ 2.97188, 1.91563 ] [ 3, 2.2 ] [ 3.1875, 1.9625 ] 17次 [ 2.97188, 1.91563 ] [ 2.88516, 2.10547 ] [ 3, 2.2 ] 18次 [ 2.97188, 1.91563 ] [ 2.85703, 1.82109 ] [ 2.88516, 2.10547 ] 19次 [ 2.97188, 1.91563 ] [ 2.8998, 1.98691 ] [ 2.85703, 1.82109 ] 20次 [ 2.97188, 1.91563 ] [ 3.01465, 2.08145 ] [ 2.8998, 1.98691 ] 21次 [ 2.97188, 1.91563 ] [ 3.01465, 2.08145 ] [ 3.08672, 2.01016 ] 22次 [ 2.94653, 1.99272 ] [ 2.97188, 1.91563 ] [ 3.01465, 2.08145 ] 23次 [ 2.98693, 2.01781 ] [ 2.94653, 1.99272 ] [ 2.97188, 1.91563 ] 最好点为[ 2.98693, 2.01781 ] 精度为:0.1函数值为:-6.9992824次 [ 2.98693, 2.01781 ] [ 2.9693, 1.96045 ] [ 2.94653, 1.99272 ] 25次 [ 3.0097, 1.98553 ] [ 2.98693, 2.01781 ] [ 2.9693, 1.96045 ] 26次 [ 3.01282, 2.02228 ] [ 3.0097, 1.98553 ] [ 2.98693, 2.01781 ] 27次 [ 3.01282, 2.02228 ] [ 3.0097, 1.98553 ] [ 3.02342, 1.99696 ] 28次 [ 2.99909, 2.01086 ] [ 3.01282, 2.02228 ] [ 3.0097, 1.98553 ] 29次 [ 3.00782, 2.00105 ] [ 2.99909, 2.01086 ] [ 3.01282, 2.02228 ] 30次 [ 3.00782, 2.00105 ] [ 2.9941, 1.98963 ] [ 2.99909, 2.01086 ] 31次 [ 3.00003, 2.0031 ] [ 3.00782, 2.00105 ] [ 2.9941, 1.98963 ] 32次 [ 3.00003, 2.0031 ] [ 3.00782, 2.00105 ] [ 3.00884, 2.0083 ] 最好点为[ 3.00003, 2.0031 ] 精度为:0.01函数值为:-6.9999933次 [ 3.00003, 2.0031 ] [ 2.99901, 1.99585 ] [ 3.00782, 2.00105 ] 34次 [ 3.00003, 2.0031 ] [ 2.99901, 1.99585 ] [ 2.99537, 1.99869 ] 35次 [ 3.00003, 2.0031 ] [ 3.00367, 2.00026 ] [ 2.99901, 1.99585 ] 36次 [ 3.00043, 1.99877 ] [ 3.00003, 2.0031 ] [ 3.00367, 2.00026 ] 37次 [ 3.00043, 1.99877 ] [ 2.99851, 2.00127 ] [ 3.00003, 2.0031 ] 38次 [ 3.00043, 1.99877 ] [ 2.99851, 2.00127 ] [ 2.99891, 1.99693 ] 39次 [ 3.00043, 1.99877 ] [ 2.99975, 2.00156 ] [ 2.99851, 2.00127 ] 40次 [ 3.00043, 1.99877 ] [ 2.99975, 2.00156 ] [ 3.00167, 1.99906 ] 最好点为[ 2.9993, 2.00071 ] 精度为:0.001函数值为:-741次 [ 2.9993, 2.00071 ] [ 3.00043, 1.99877 ] [ 2.99975, 2.00156 ] 42次 [ 2.99992, 1.99883 ] [ 2.9993, 2.00071 ] [ 3.00043, 1.99877 ] 43次 [ 2.9992, 2.00028 ] [ 2.99992, 1.99883 ] [ 2.9993, 2.00071 ] 44次 [ 2.99969, 1.99897 ] [ 2.9992, 2.00028 ] [ 2.99992, 1.99883 ] 45次 [ 2.99921, 2.00002 ] [ 2.99969, 1.99897 ] [ 2.9992, 2.00028 ] 46次 [ 2.99958, 1.99911 ] [ 2.99921, 2.00002 ] [ 2.99969, 1.99897 ] 47次 [ 2.99924, 1.99986 ] [ 2.99958, 1.99911 ] [ 2.99921, 2.00002 ] 48次 [ 2.99951, 1.99922 ] [ 2.99924, 1.99986 ] [ 2.99958, 1.99911 ] 49次 [ 2.99928, 1.99975 ] [ 2.99951, 1.99922 ] [ 2.99924, 1.99986 ] 最好点为[ 2.99947, 1.9993 ] 精度为:0.0001函数值为:-750次 [ 2.99947, 1.9993 ] [ 2.99928, 1.99975 ] [ 2.99951, 1.99922 ] 51次 [ 2.9993, 1.99968 ] [ 2.99947, 1.9993 ] [ 2.99928, 1.99975 ] 52次 [ 2.9993, 1.99968 ] [ 2.99944, 1.99936 ] [ 2.99947, 1.9993 ] 53次 [ 2.99932, 1.99963 ] [ 2.9993, 1.99968 ] [ 2.99944, 1.99936 ] 54次 [ 2.99938, 1.9995 ] [ 2.99932, 1.99963 ] [ 2.9993, 1.99968 ] 55次 [ 2.99938, 1.9995 ] [ 2.9994, 1.99945 ] [ 2.99932, 1.99963 ] 56次 [ 2.99938, 1.9995 ] [ 2.99936, 1.99955 ] [ 2.9994, 1.99945 ] 57次 [ 2.99938, 1.9995 ] [ 2.99936, 1.99955 ] [ 2.99935, 1.99957 ] 58次 [ 2.99938, 1.9995 ] [ 2.99938, 1.99949 ] [ 2.99936, 1.99955 ] 59次 [ 2.99938, 1.9995 ] [ 2.99937, 1.99953 ] [ 2.99938, 1.99949 ] 60次 [ 2.99938, 1.9995 ] [ 2.99936, 1.99954 ] [ 2.99937, 1.99953 ] 61次 [ 2.99937, 1.99951 ] [ 2.99938, 1.9995 ] [ 2.99936, 1.99954 ] 62次 [ 2.99937, 1.99951 ] [ 2.99938, 1.99949 ] [ 2.99938, 1.9995 ] 63次 [ 2.99938, 1.9995 ] [ 2.99937, 1.99951 ] [ 2.99938, 1.99949 ] 64次 [ 2.99937, 1.99954 ] [ 2.99938, 1.9995 ] [ 2.99937, 1.99951 ] 65次 [ 2.99938, 1.99954 ] [ 2.99937, 1.99954 ] [ 2.99938, 1.9995 ] 最好点为[ 2.99938, 1.99954 ] 精度为:1e-05函数值为:-7
感谢您的阅读,生活愉快~
作者:林-兮
出处:http://www.cnblogs.com/lv-anchoret/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。
共同学习,写下你的评论
评论加载中...
作者其他优质文章