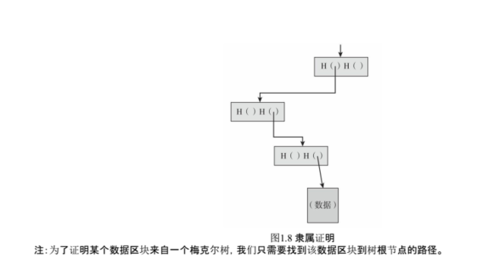
隶属证明
原文精选:与我们之前建立的区块链不同,梅克尔树的另一个特点是它可以实现简洁的隶属证明。假设某人想要证明某个数据区块隶属于梅克尔树。同样地,我们只记住树根节点,然后他需要展示给我们数据块信息,以及从该数据区块通向树根节点的那些区块,我们可以忽略树的其余部分,这样做是因为这些区块已经足够让我们验证通往树根节点过程中所有的哈希值。其工作原理图解参见图1.8。
如果整棵树上有n个节点,只需要展示约log(n)个项目,因为每个步骤仅需要计算子区块的哈希值,验证过程需要时间约为log(n)。因此,即使梅克尔树包含大量的区块,我们仍可以在相对较短时间内证明隶属关系。因此,验证需要花的时间和涉及空间(树节点)与log(n)同级。
一个排序梅克尔树是把底层的数据通过某些排序得到的梅克尔树,这里排序规则可以是字母表排序、词典排序、数字化排序,或者其他约定的排序方式。
读书笔记:
1,如果想要证明某个数据区块隶属于梅克尔树,梅克尔树可以实现简洁的隶属证明。
2,我们可以忽略其他信息,只寻找该数据区块到树根节点的路径。
3,即使梅克尔树包含大量的区块,我们仍可以在相对较短时间内证明隶属关系,因为只需要验证跟该数据有关的区块就可以了。
4,一个排序梅克尔树是把底层的数据通过某些排序得到的梅克尔树,排序方式非常多样化。
非隶属证明
原文精选:有了排序梅克尔树,我们可以在一个对数复杂度的条件下验证某一个数据区块并非来自某梅克尔树。也就是说,我们可以证明某个特定区块不属于梅克尔树,而我们只是简单通过展示被验证区块之前的区块路径,以及被验证区块之后的区块路径,就可以达到目的。如果之前、之后两个区块在树上是连续的,那么这说明了被验证区块与该梅克尔树之间是非隶属关系。因为被验证区块确实隶属于梅克尔树,它需要在两个条目之间,而如果两个条目是连续的话,二者之间则并没有空间。
我们讨论过在链表及二叉树中使用哈希指针,但更广泛地说,我们可以在任何以指针为基础的数据结构中使用哈希指针,条件是数据结构不存在循环。如果数据结构中存在循环,那么我们将不能使所有哈希值得到匹配。想一下,在一个非循环的数据结构中,我们可以在靠近节点的地方开始,或者在没有指针的数据区块开始,计算其哈希值,然后从后往前进行计算。但是在一个有循环结构的网络中,并没有一个根节点,可以让我们去追溯。
因此,试想另一个例子,我们可以建立一个哈希指针定向的非循环图。我们能够在该图中非常有效地验证隶属关系,同时也方便计算。这样的哈希指针使用方式是一个常见技巧。
读书笔记:
1,有了排序梅克尔树,我们同样可以证明某个特定区块不属于该梅克尔树。
2,只要数据结构不存在循环,我们就可以在任何以指针为基础的数据结构中使用哈希指针。
3,如果在一个有循环结构的网络中,就不存在根节点让我们去追溯了。
4,可以建立一个哈希指针定向的非循环图,那么就能够非常有效地验证隶属关系。
一叶之秋带你一分钟速读经典书籍,每天一分钟(只需阅读读书笔记部分),天天获新知。
作者:全职高手一叶之秋
链接:https://www.jianshu.com/p/a52f98d40c19
共同学习,写下你的评论
评论加载中...
作者其他优质文章