神经网络学习率（learning rate）的衰减

一、学习率衰减的概念和必要性

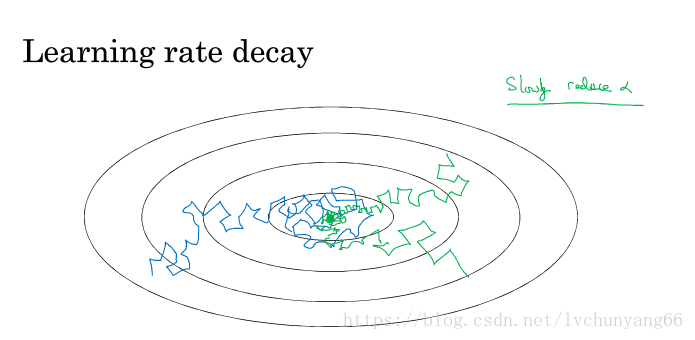
学习率过大，在算法优化的前期会加速学习，使得模型更容易接近局部或全局最优解。但是在后期会有较大波动，甚至出现损失函数的值围绕最小值徘徊，波动很大，始终难以达到最优，如下图蓝色曲线所示。所以引入学习率衰减的概念，直白点说，就是在模型训练初期，会使用较大的学习率进行模型优化，随着迭代次数增加，学习率会逐渐进行减小，保证模型在训练后期不会有太大的波动，从而更加接近最优解，如下图中上面一条绿色曲线所示。

当学习率过大，以J(X)=X^2为例，学习率始终为1，梯度下降算法的运行过程：

可以看到无论进行多少轮迭代，参数始终在5和-5之间摇摆，而不是收敛到一个极小值。

二、学习率衰减的类型

学习率衰减的类型有很多种，大致可以分为两类：

一是通过人为经验进行设定，如到达多少轮后，设定具体的学习率为多少；二是随着迭代轮数的增加学习率自动发生衰减，这类有比较常用的指数型衰退，具体算法如下图

其中decayed_learning_rate为每一轮优化时使用的学习率，learning_rate为事先设定的初始学习率，decay_rate为衰减系数，decay_steps为衰减速度。

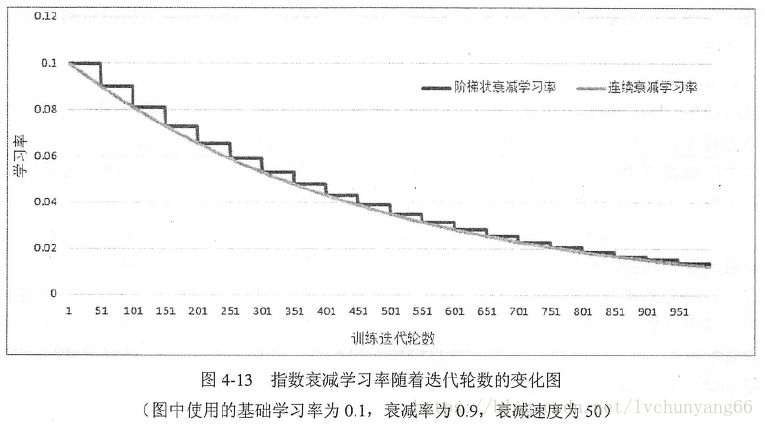
在tensorflow中指数型衰减通过调用tf.train.exponential_decay(learning_rate, global_step, decay_steps, decay_rate, staircase=False, name=None)实现。这里介绍一下decay_steps，若decay_steps=100，即表示100轮迭代后进行一次衰减，staircase=True时，global_step/decay_steps会被转化为整数，这使得学习率呈阶梯型下降（如下图黑色），若staircase=False，下图灰色为连续型衰减学习率。

原文出处