在比较两种不同的机器学习算法或比较相同的算法与不同的配置时,收集一组结果是一个好习惯。
考虑到大多数机器学习算法的随机性,重复每个实验运行30次或更多次,可以得到一组结果,从中可以计算平均期望性能。
如果两种算法或配置的平均期望性能不同,您怎么知道这种差异是显着的,并且有多重要?
统计显着性检验是帮助解释机器学习实验结果的重要工具。此外,这些工具的发现可以帮助您更好,更自信地呈现您的实验结果,并为您的预测建模问题选择正确的算法和配置。
在本教程中,您将了解如何使用Python中的统计显着性测试来研究和解释机器学习实验结果。
完成本教程后,您将知道:
如何应用正态性测试来确认您的数据是否正常分布。
如何对正态分布结果应用参数统计显着性检验。
如何将非参数统计显着性检验应用于更复杂的结果分布。
让我们开始吧。

教程概述
本教程分为6个部分。他们是:
生成示例数据
摘要统计
正态性测试
比较高斯结果的手段
高斯结果与不同方差的比较均值
比较非高斯结果的手段
本教程假定Python 2或3以及带有NumPy,Pandas和Matplotlib的SciPy环境。
生成示例数据
情况是,你有来自两个算法的实验结果或两个不同的相同算法的配置。
每个算法在测试数据集上被多次试验,并且已经收集了一个技能评分。我们剩下两个技能分数。
我们可以通过产生两个分布在稍微不同的方式上的高斯随机数的总体来模拟这个问题。
下面的代码生成第一个算法的结果。总共1000个结果存储在名为results1.csv的文件中。结果从高斯分布绘制,平均值为50,标准偏差为10。
from numpy.random import seedfrom numpy.random import normalfrom numpy import savetxt
# define underlying distribution of results
mean = 50stev = 10# generate samples from ideal distributionseed(1)results = normal(mean, stev, 1000)# save to ASCII filesavetxt('results1.csv', results)下面是results1.csv的前5行数据的一小段。
6.624345363663240960e+014.388243586349924641e+014.471828247736544171e+013.927031377843829318e+015.865407629324678851e+01...
现在我们可以生成第二个算法的结果。我们将使用相同的方法,并从略微不同的高斯分布(平均值为60,具有相同的标准偏差)中得出结果。结果写入results2.csv。
from numpy.random import seedfrom numpy.random import normalfrom numpy import savetxt
# define underlying distribution of results
mean = 60stev = 10# generate samples from ideal distributionseed(1)results = normal(mean, stev, 1000)# save to ASCII filesavetxt('results2.csv', results)下面是results2.csv的前5行的示例。
7.624345363663240960e+015.388243586349924641e+015.471828247736544171e+014.927031377843829318e+016.865407629324678851e+01...
展望未来,我们将假装我们不知道任何一组结果的基本分布。
我选择每个实验1000个结果的人口任意。使用30或100个结果的群体来获得适当的好估计(例如,低标准误差)更为现实。
不要担心,如果你的结果不是高斯; 我们将看看这些方法如何分解非高斯数据以及使用替代方法。
摘要统计
收集结果后的第一步是查看一些汇总统计数据,并更多地了解数据的分布情况。
这包括检查数据的汇总统计和图表。
以下是完整的代码清单,用于查看两组结果的汇总统计信息。
from pandas import DataFramefrom pandas import read_csvfrom matplotlib import pyplot
# load results file
results = DataFrame()results['A'] = read_csv('results1.csv', header=None).values[:, 0]results['B'] = read_csv('results2.csv', header=None).values[:, 0]# descriptive statsprint(results.describe())# box and whisker plot
results.boxplot()pyplot.show()# histogram
results.hist()pyplot.show()该示例加载两组结果,并通过打印汇总统计开始。results1.csv中的数据称为“A”,为简洁起见,将results2.csv中的数据称为“B”。
我们将假定数据表示测试数据集的错误分数,并且将分数最小化是目标。
我们可以看到平均A(50.388125)比B(60.388125)好。我们也可以在中位数(第50百分位)看到同样的故事。看看标准偏差,我们也可以看到,两个分布都有相似的(相同的)分布。
A B count 1000.000000 1000.000000mean 50.388125 60.388125std 9.814950 9.814950min 19.462356 29.46235625% 43.998396 53.99839650% 50.412926 60.41292675% 57.039989 67.039989max 89.586027 99.586027
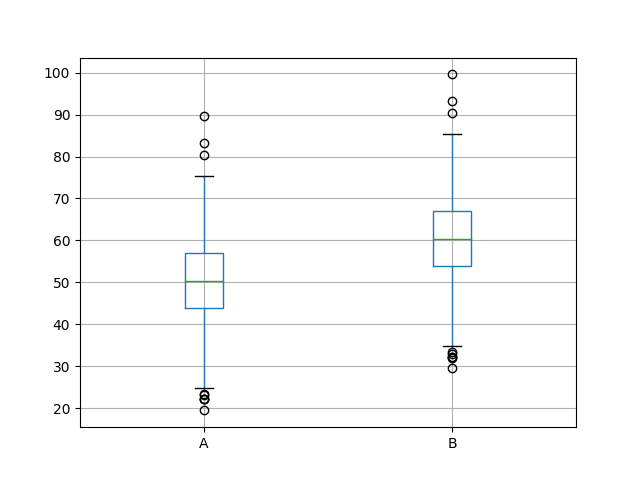
接下来,创建一个盒子和胡须图,比较两组结果。该框捕获中间50%的数据,异常值显示为点,绿线显示中位数。我们可以看到,这两个数据确实有一个类似的分布,似乎在中位数左右是对称的。
A的效果比B好看。
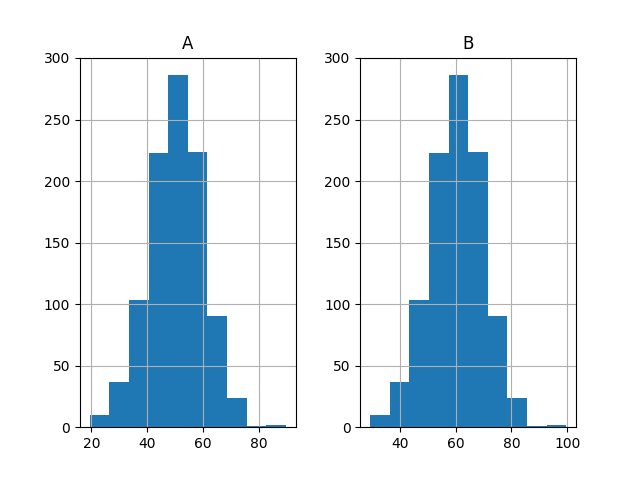
最后,绘制两组结果的直方图。
这些图表强烈地表明这两组结果都是从高斯分布中得出的。
正态性测试
从高斯分布中得到的数据可以更容易地工作,因为有许多专门为这种情况设计的工具和技术。
我们可以使用统计检验来确认从两个分布中得到的结果是高斯(也称为正态分布)。
在SciPy中,这是normaltest() 函数。
从文档中,测试描述为:
测试样本是否与正态分布不同。
测试(H0)的零假设或默认期望是统计量描述正态分布。
如果p值大于0.05,我们接受这个假设。如果p值<= 0.05,我们拒绝这个假设。在这种情况下,我们相信95%的置信度是不正常的。
下面的代码加载results1.csv并确定数据是否有可能是高斯的。
from pandas import read_csvfrom scipy.stats import normaltestfrom matplotlib import pyplot
result1 = read_csv('results1.csv', header=None)value, p = normaltest(result1.values[:,0])print(value, p)if p >= 0.05:
print('It is likely that result1 is normal')else:
print('It is unlikely that result1 is normal')首先运行该示例打印出计算的统计量和统计量从高斯分布计算出的p值。
我们可以看到results1.csv很可能是高斯的。
2.99013078116 0.224233941463It is likely that result1 is normal
我们可以用results2.csv中的数据重复同样的测试。
下面提供了完整的代码清单。
from pandas import read_csvfrom scipy.stats import normaltestfrom matplotlib import pyplot
result2 = read_csv('results2.csv', header=None)value, p = normaltest(result2.values[:,0])print(value, p)if p >= 0.05:
print('It is likely that result2 is normal')else:
print('It is unlikely that result2 is normal')运行该示例提供了相同的统计p值和结果。
两组结果都是高斯的。
2.99013078116 0.224233941463It is likely that result2 is normal
比较高斯结果的均值
两组结果都是高斯的,方差相同; 这意味着我们可以使用学生t检验来查看两个分布的均值之间的差异是否具有统计显着性。
在SciPy中,我们可以使用ttest_ind()函数。
测试描述如下:
计算两个独立样本得分的T检验。
测试的无效假设(H0)或默认期望是两个样本都来自同一群体。如果我们接受这个假设,那就意味着手段之间没有显着差异。
如果我们得到<= 0.05的p值,这意味着我们可以拒绝零假设,而且手段有95%的置信度显着不同。这意味着对于100个样本中的95个相似的样本,手段将显着不同,在100个案例中有5个不同。
除了数据是高斯分布外,这个统计检验的重要假设是两个分布具有相同的方差。我们知道这是从上一步中查看描述性统计数据的情况。
下面提供了完整的代码清单。
from pandas import read_csvfrom scipy.stats import ttest_indfrom matplotlib import pyplot
# load results1
result1 = read_csv('results1.csv', header=None)values1 = result1.values[:,0]# load results2
result2 = read_csv('results2.csv', header=None)values2 = result2.values[:,0]# calculate the significance
value, pvalue = ttest_ind(values1, values2, equal_var=True)print(value, pvalue)if pvalue > 0.05:
print('Samples are likely drawn from the same distributions (accept H0)')else:
print('Samples are likely drawn from different distributions (reject H0)')运行该示例将打印统计信息和p值。我们可以看到p值远低于0.05。
事实上,它是如此之小,我们有一个接近确定的手段之间的差异是统计显着的。
-22.7822655028 2.5159901708e-102Samples are likely drawn from different distributions (reject H0)
高斯结果与不同方差的比较均值
如果两组结果的平均值相同,但方差是不同的呢?
我们无法按照原样使用Student t检验。事实上,我们将不得不使用一个名为韦尔奇的t检验的修改版本的测试。
在SciPy中,这与ttest_ind()函数是一样的,但我们必须将“ equal_var ”参数设置为“ False ”,以指示差异不相等。
我们可以用一个例子来证明这一点,即我们用非常相似的方法(50 vs 51)和非常不同的标准差(1 vs 10)产生两组结果。我们将生成100个样本。
from numpy.random import seedfrom numpy.random import normalfrom scipy.stats import ttest_ind
# generate resultsseed(1)n = 100values1 = normal(50, 1, n)values2 = normal(51, 10, n)# calculate the significance
value, pvalue = ttest_ind(values1, values2, equal_var=False)print(value, pvalue)if pvalue > 0.05:
print('Samples are likely drawn from the same distributions (accept H0)')else:
print('Samples are likely drawn from different distributions (reject H0)')运行该示例将打印测试统计信息和p值。
我们可以看到,有很好的证据(接近99%)是从不同的分布中抽取样本,手段有很大的不同。
-2.62233137406 0.0100871483783Samples are likely drawn from different distributions (reject H0)
分布越接近,所需的样本就越大。
我们可以通过计算每组结果的不同大小子样本的统计检验来证明这一点,并根据样本大小绘制p值。
我们预计随着样本量的增加,p值会变小。我们也可以在95%的水平(0.05)画出一条线,并显示样本的大小足够大以表明这两个种群有显着差异。
from numpy.random import seedfrom numpy.random import normalfrom scipy.stats import ttest_indfrom matplotlib import pyplot # generate resultsseed(1)n = 100values1 = normal(50, 1, n)values2 = normal(51, 10, n)# calculate p-values for different subsets of results pvalues = list()for i in range(1, n+1): value, p = ttest_ind(values1[0:i], values2[0:i], equal_var=False) pvalues.append(p)# plot p-values vs number of results in sample pyplot.plot(pvalues)# draw line at 95%, below which we reject H0 pyplot.plot([0.05 for x in range(len(pvalues))], color='red')pyplot.show()
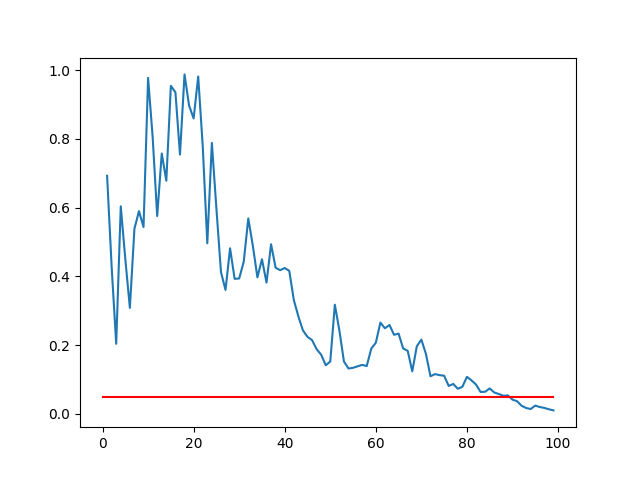
运行示例将创建一个p值与样本大小的折线图。
我们可以看到,对于这两组结果,在我们有95%的置信度方法显着不同(蓝线与红线相交处)之前,样本量必须在90左右。
比较非高斯结果的手段
如果我们的数据不是高斯的话,我们不能使用Student t检验或者Welch的t检验。
我们可以用于非高斯数据的另一个统计显着性检验被称为Kolmogorov-Smirnov检验。
在SciPy中,这被称为ks_2samp()函数。
在文档中,这个测试被描述为:
这是对两个独立样本从相同的连续分布中抽取的零假设的双面测试。
这个测试可以在高斯数据上使用,但是统计功率较小,可能需要大量的样本。
我们可以证明对两组非高斯分布结果的统计显着性的计算。我们可以生成两组重叠均匀分布(50到60和55到65)的结果。这些结果将分别具有大约55和60的不同平均值。
下面的代码生成两组100个结果,并使用Kolmogorov-Smirnov检验来证明总体均值之间的差异是统计显着的。
from numpy.random import seedfrom numpy.random import randintfrom scipy.stats import ks_2samp
# generate resultsseed(1)n = 100values1 = randint(50, 60, n)values2 = randint(55, 65, n)# calculate the significance
value, pvalue = ks_2samp(values1, values2)print(value, pvalue)if pvalue > 0.05:
print('Samples are likely drawn from the same distributions (accept H0)')else:
print('Samples are likely drawn from different distributions (reject H0)')运行该示例将打印统计信息和p值。
p值非常小,这表明几乎可以肯定的是两个人群之间的差异是显着的。
0.47 2.16825856737e-10Samples are likely drawn from different distributions (reject H0)
概要
在本教程中,您了解了如何使用统计显着性测试来解释机器学习结果。
您可以使用这些测试来帮助您自信地选择一个机器学习算法而不是另一个机器学习算法或一组配置参数。
你了解到:
如何使用常态测试来检查您的实验结果是否为高斯。
如何使用统计检验来检查平均结果之间的差异对于具有相同和不同方差的高斯数据是否显着。
如何使用统计测试来检查平均结果之间的差异是否对非高斯数据有意义。
本文的版权归 老人雨何 所有,如需转载请联系作者。
原文链接在腾讯云
共同学习,写下你的评论
评论加载中...
作者其他优质文章





