首页手记 Python进阶量化交易场外篇3—&mda...

Python进阶量化交易场外篇3——最大回撤评价策略风险

标签：

Python 机器学习人工智能

新年伊始，很荣幸笔者的《教你用 Python 进阶量化交易》专栏在慕课专栏板块上线了，欢迎大家订阅！为了能够提供给大家更轻松的学习过程，笔者在专栏内容之外会陆续推出一些手记来辅助同学们学习本专栏内容，因此同学们无需担心专栏内容在学习上的困难，更多的是明确自己学习的目的即可。当然笔者也欢迎同学们踊跃留言，说出自己想扩展的知识点，笔者会根据同学们的意愿选择性的推出一些内容。

在第一篇《管理概率==理性交易》中笔者结合一个简单的市场模型介绍了为什么在没有概率优势的前提下参与交易会亏钱，其实股票交易和玩一个游戏、做一个项目理念是相通的，需要章法、需要制定策略，否则就和抛硬币赌博一样一样的，用量化交易可以帮助我们管理好概率，更理性的去下单。

在第二篇《线性回归拟合股价沉浮》中笔者在专栏《股票交易策略开发：走势线性回归选股策略》小节的基础上对线性回归方法的策略应用做进一步的扩展介绍。由于线性回归作用于股票收盘价的整个周期，前后两段完全相反的周期会彼此作用，最终影响拟合的角度值，于是笔者设定窗口期用移动窗口的方式拟合股价的走势，寻找角度曲线的拐点以预示新一轮的反转走势，给大家提供一个衍生的策略思路。

本次场外篇笔者在专栏《18、股票交易数据可视化：买卖区间下策略收益绘制》的基础上对策略的最大回撤指标做一定的扩展介绍。最大回撤属于判断策略风险高低的指标，用来描述买入股票后，在策略出现最糟糕的情况下会损失多少钱，这也直接关系到《21、股票交易策略开发：ATR止盈止损风险策略》小节中对于风险策略中止盈止损因子的设定。

我们知道投资是有风险的，那么如何去衡量这个风险呢？最大回撤率就是一种直观的将风险切实量化的指标。最大回撤率计算公式：max（1-当日收盘价/当日之前最高价）*100％【（最高价-最低价）/最高价】。举个例子，在股票最高价2元买入，近半年内，股价下跌到最低点1.6元，最大亏损0.4元，那么这近半年最大回撤率=1-1.6/2×100％，结果是20％。显而易见，最大回撤率越小越好，因为回撤与风险成正比，回撤越大，风险也就越高。最大回撤的概念虽然直观，但在程序中到底应该怎么实现计算呢？

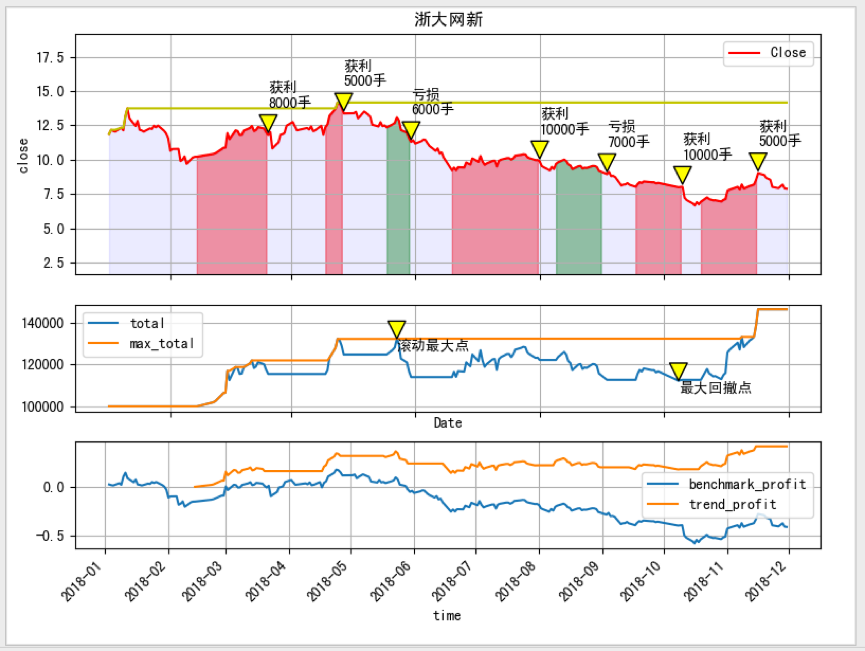
我们延续专栏《18、股票交易数据可视化：买卖区间下策略收益绘制》的内容，计算浙大网新股价的最大回撤率和应用策略后资金曲线的最大回撤率。以计算资金曲线最大回撤率为例，首先使用expanding() 计算资金曲线的滚动最大值，也就是截至当前时间，资金曲线的最大值，图中的橙色曲线所示。

接着，将资金曲线与资金曲线滚动最大值矢量相除，即得到回撤后资金剩余的百分比，也就是资金曲线在滚动最大值之后剩余资金的百分比，对剩余资金百分比从小到大排序，那么第一行就包含了回撤后资金剩余百分比的最小值，1-资金剩余百分比最小值即为资金曲线最大回撤率。

以下为计算资金曲线最大回撤率实现代码，同理计算股价曲线最大回撤率与此类同：

#expanding()计算资金曲线当前的滚动最高值
stock_df['max_total'] = stock_df['total'].expanding().max()
#计算资金曲线在滚动最高值之后所回撤的百分比
stock_df['per_total'] = stock_df['total']/stock_df['max_total']
min_point_total = stock_df.sort_values(by=['per_total']).iloc[[0], stock_df.columns.get_loc('per_total')]
print(min_point_total)
max_point_total = stock_df[stock_df.index <= min_point_total.index[0]].sort_values\         
(by=['total'],ascending=False).iloc[[0],stock_df.columns.get_loc('total')]
print("最大资金回撤%5.2f%%从%s开始至%s结束"%((1-min_point_total.values),\
max_point_total.index[0],min_point_total.index[0]))