首页手记猿考研之数据结构篇二（树型结构与图）

猿考研之数据结构篇二（树型结构与图）

标签：

数据结构算法算法与数据结构

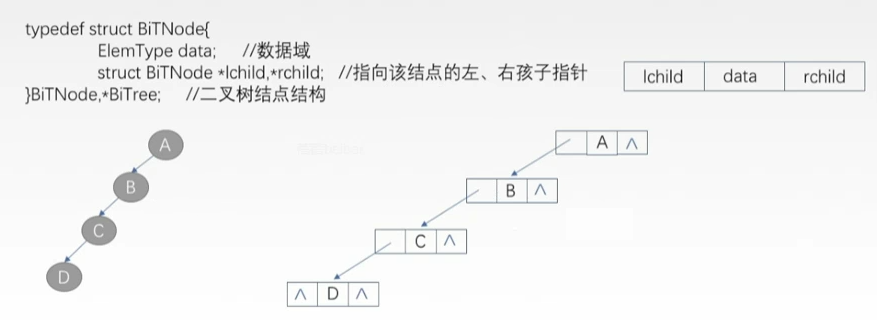
树

树是N（N≥0）个结点的有限集合，N=0时，称为空树，这是一种特殊情况。树是递归定义的结构。在任意一棵非空树中应满足：
- 1)有且仅有一个特定的称为根的结点。
- 2）当N>1时，其余结点可分为m(m>0)个互不相交的有限集合T1，T2.….Tm,其中每一个集合本身又是一棵树，并且称为根结点的子树。

概念

结点
根结点：树只有一个根结点
结点的度：结点拥有的子树的数量
- 度为0：叶子结点或者终端结点
- 度不为0：分支临点或者非终端结点。
  - 分支终端中除去根节点也成为内部节点
树的度：树中所有结点的度数的最大值
结点关系
- 祖先结点
  - 根结点到该结点的唯一路径上的任意结点
- 子孙结点
- 双亲结点
  - 根结点到该节点的唯一路径上最接近该节点的节点
- 孩子结点
- 兄弟结点
  - 有相同双亲结点的结点
层次
- 层款：根为第一层，它的孩子为第二层，以此类推
- 结点的深度：根结点开始自顶向下累加
- 结点的高度：叶结点开始自底向上累加
- 树的高度（深度）：树中结点的最大层数

树的性质

树中的结点数等于所有结点的度数加1。
- 证明：不难想象，除根结点以外，每个结点有且仅有一个指向它的前驱结点。也就是说每个结点和指向它的分支一一对应。
- 假设树中一共有b个分支，那么除了根结点，整个树就包含有b个结点，所以整个树的结点数就是这b个结点加上根结点，设为n，则n=b+1。而分支数b也就是所有结点的度数，证毕。
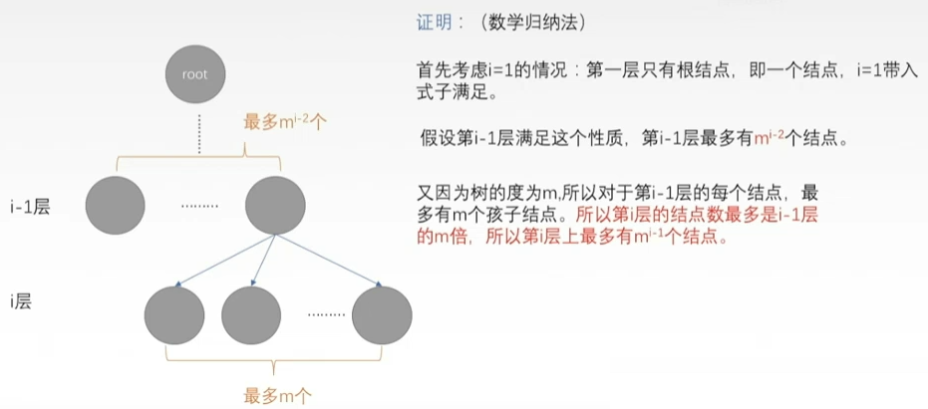
度为m的树中第i层上至多有m^(i-1)个结点（i≥1）
高度为h的m叉树至多有（m^h -1)/(m-1）个结点
具有n个结点的m叉树的最小高度为[logm(n(m-1)+1)]

树的顺序存储结构

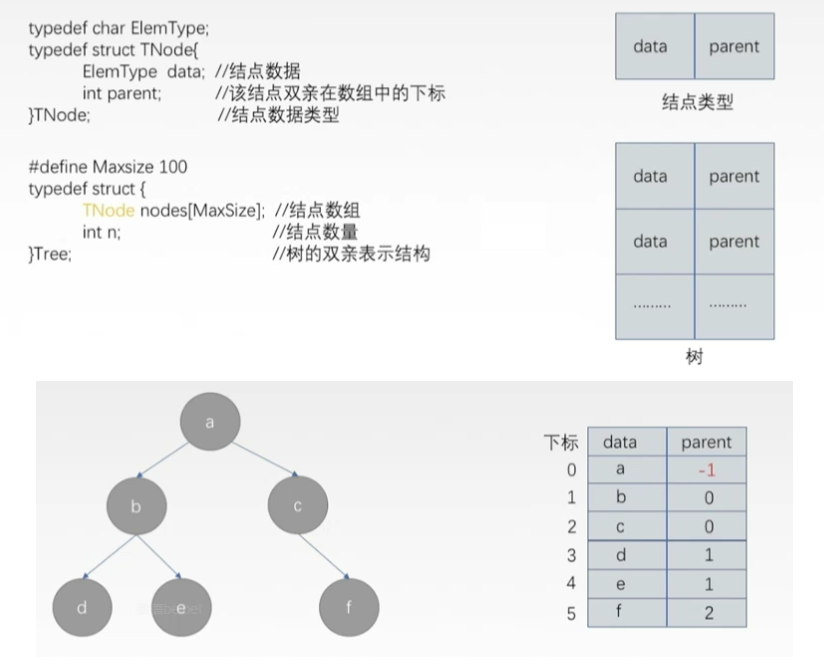
双亲表示法：用一组连续的存储空间存储树的结点，同时在每个结点中，用一个变量存储该结点的双亲结点在数组中的位置。

双亲表示法可以根据parent值找到该结点的双亲结点，时间复杂度为O(1)。
不过查找孩子节点非常麻烦

树的链式存储结构

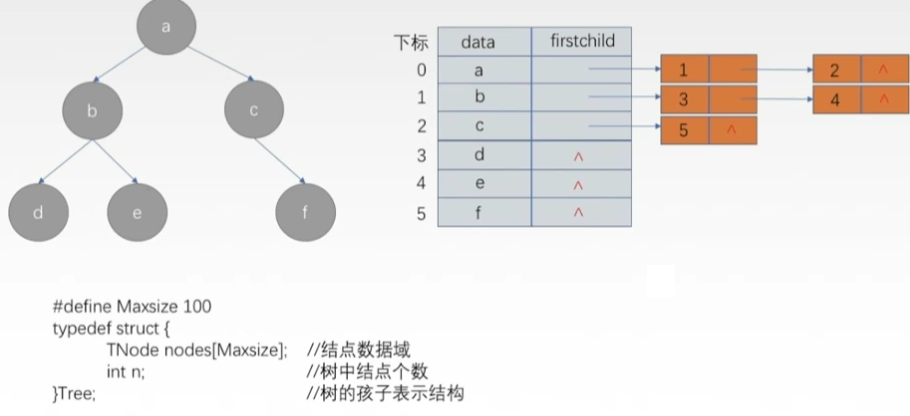
孩子表示法：
- 把每个结点的孩子结点排列起来存储成一个单链表。
- 所以n个结点就有n个链表；
- 如果是叶子结点，那这个结点的孩子单链表就是空的；
- 然后n个单链表的的头指针又存储在一个**顺序表（数组）**中。
两种结点结构类型
- 孩子链表
- 每个孩子链表的表头结点（存在数组中）
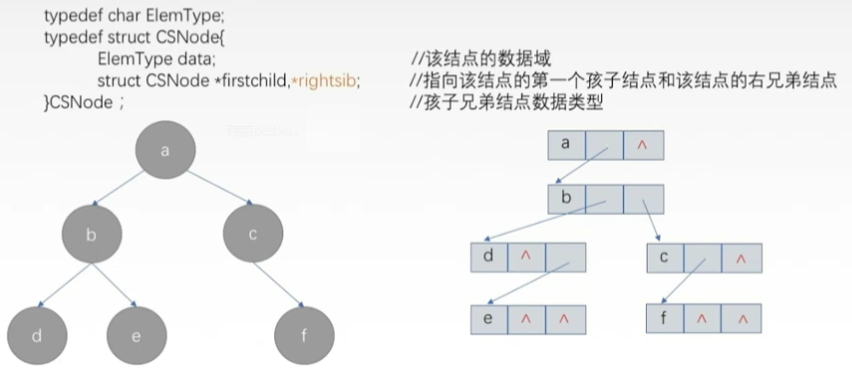
孩子兄弟表示法：
- 顾名思义就是要存储孩子结点和兄弟结点，具体来说，就是设置两个指针，分别指向该结点的第一个孩子结点和该结点的兄弟结点。

二叉树

二叉树是n（n≥0)个结点的有限集合：
或者为空二叉树，即n=0。
或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
1.每个结点最多有两棵子树。
2.左右子树有顺序
二叉树的五种基本形态：
- 1.空树
- 2.只有一个根结点
- 3.根结点只有左子树
- 4.根结点只有右子树
- 5.根结点既有左子树又有右子树

特殊二叉树

斜树
- 每一层都只有一个结点，结点数与树的深度相同
满二叉树
- 分支结点都存在左子树和右子树
- 叶子都在同一层
- 特点：
  - 非叶子结点的度一定是2
  - 相同深度二又树中满二又树的结点个数最多，叶子数最多
完全二叉树
- 完全二又树：设一个高度为h，有n个结点的二又树，当且仅当其每一个结点都与高度为h的满二又树中编号为1~n的结点一一对应时，称为完全二又树
- 和同高度满二又树的结点按层序编号是一一对应的
- 特点：
  - 1.叶子结点只可能在层次最下两层上出现且最下层的叶子结点一定集中在左部连续的位置。
  - 2.如果有度为1的结点，只可能有一个，且该结点只有左孩子而无右孩子。
  - 3.同样结点数的二又树，完全二又树的深度是最小的。

二叉树的性质

非空二叉树上叶子结点数等于度为2的结点数加1
非空二又树上第K层上至多有2^(k-1)个结点（K≥1）
高度为H的二叉树至多有2^H-1个结点（H≥1)
- 等比数列求和
具有N个（N>0)结点的完全二叉树的高度为log2(N+1)或log2N+1。

二叉树的存储结构

二叉树的顺序存储结构就是用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素。

但是对于一般的非完全二叉树，咋办？
- 比如斜树，开辟大小为15的数组却只存4个数据，为了保存二叉树的结点逻辑关系“牺牲”过大。

二叉树每个结点最多两个孩子，所以设计二又树的结点结构时考虑两个指针指向该结点的两个孩子。
两个指针，也叫二叉链表
另外还可以增加指针指向该结点的双亲结点，那这时三个指针的链表叫做三叉链表

二叉树的遍历（递归）

二叉树的遍历是指按某种次序依次访问树中的每个结点，使得每个结点均被访问一次，而且仅被访问一次。

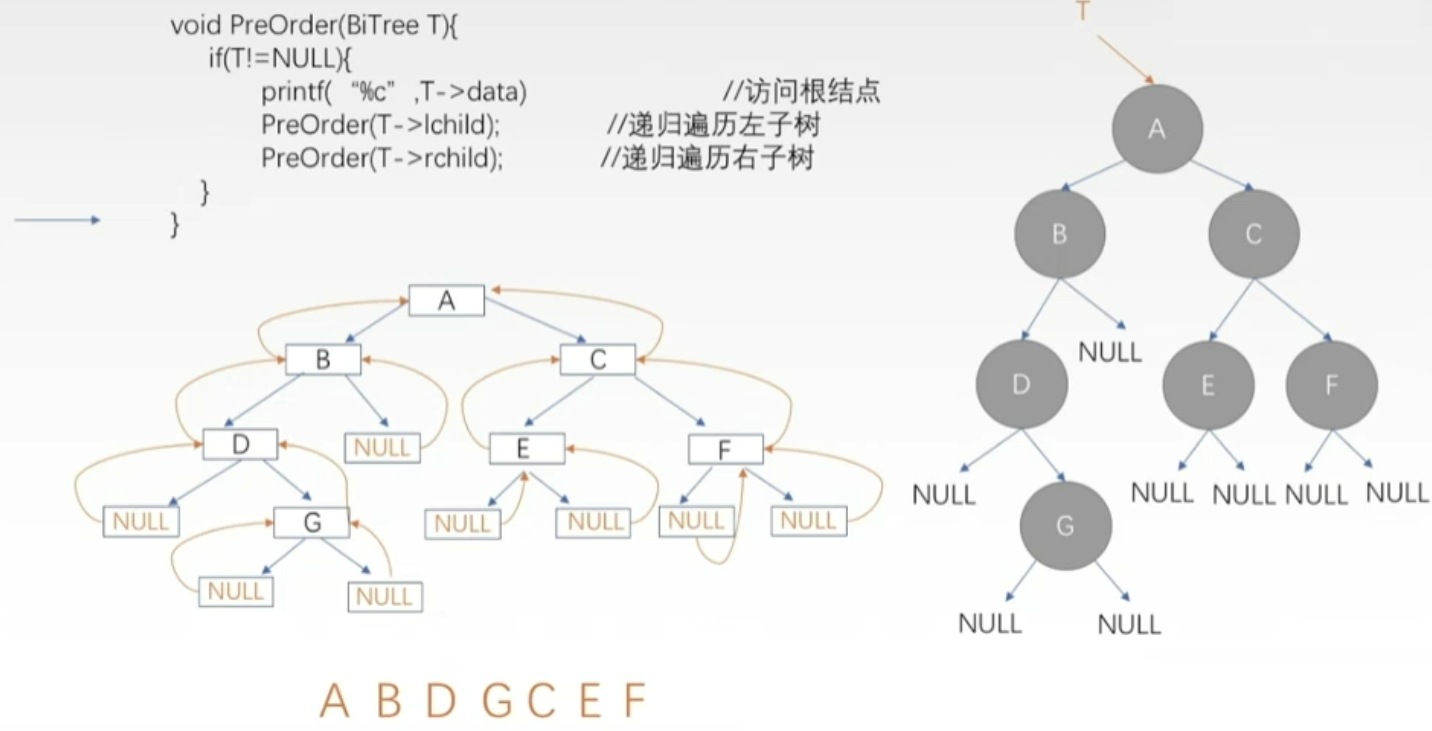
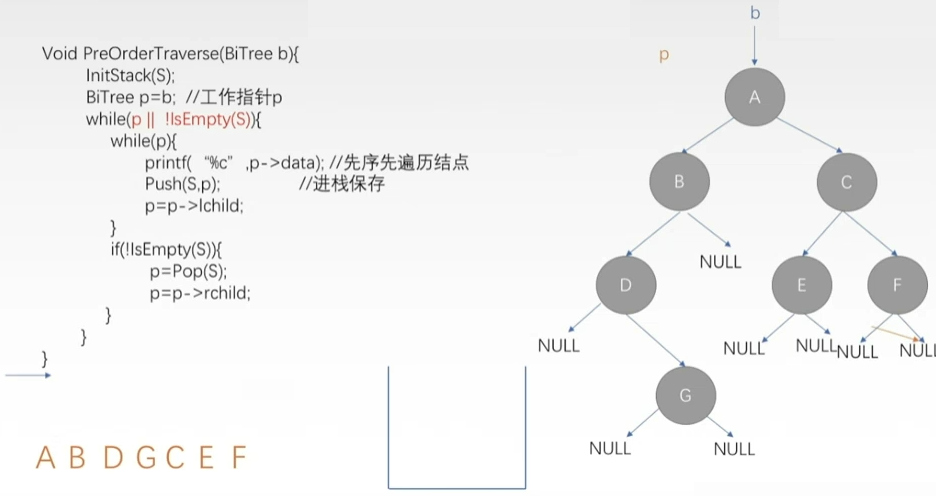
先序遍历
- 如果二叉树为空，什么也不做。否则：
  - 1）访问根结点；
  - 2）先序遍历左子树；
  - 3）先序遍历右子树。
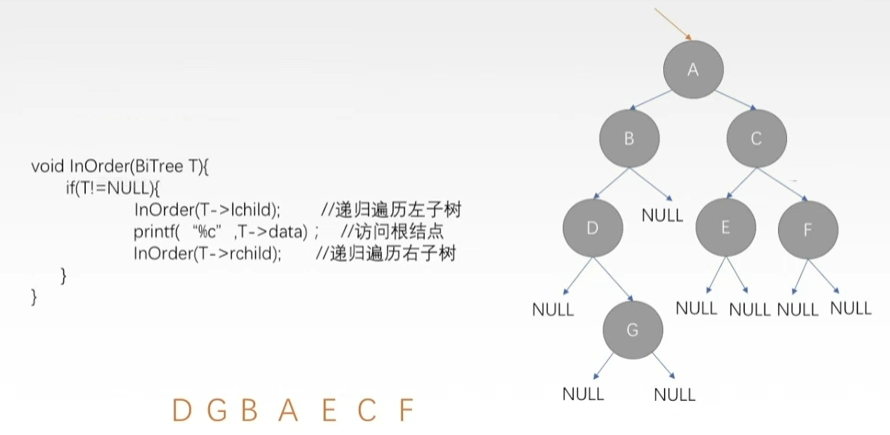
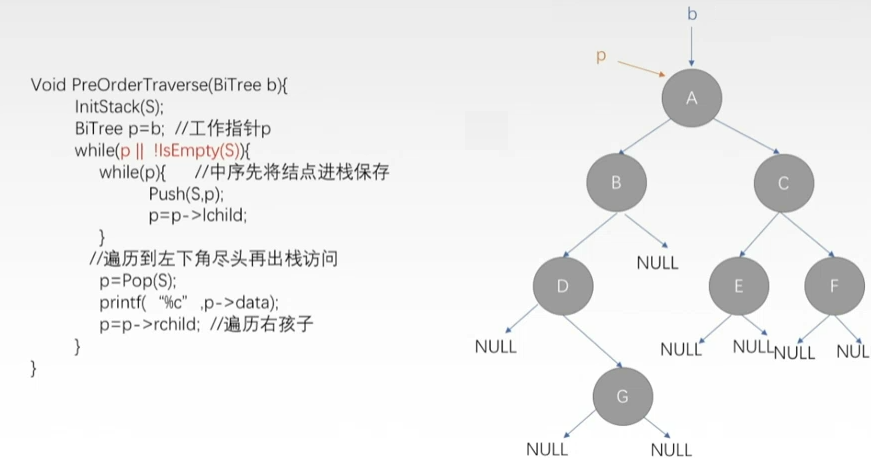
中序遍历
- 如果二叉树为空，什么也不做。否则：
  - 1）中序遍历左子树；
  - 2）访问根结点；
  - 3）中序遍历右子树。
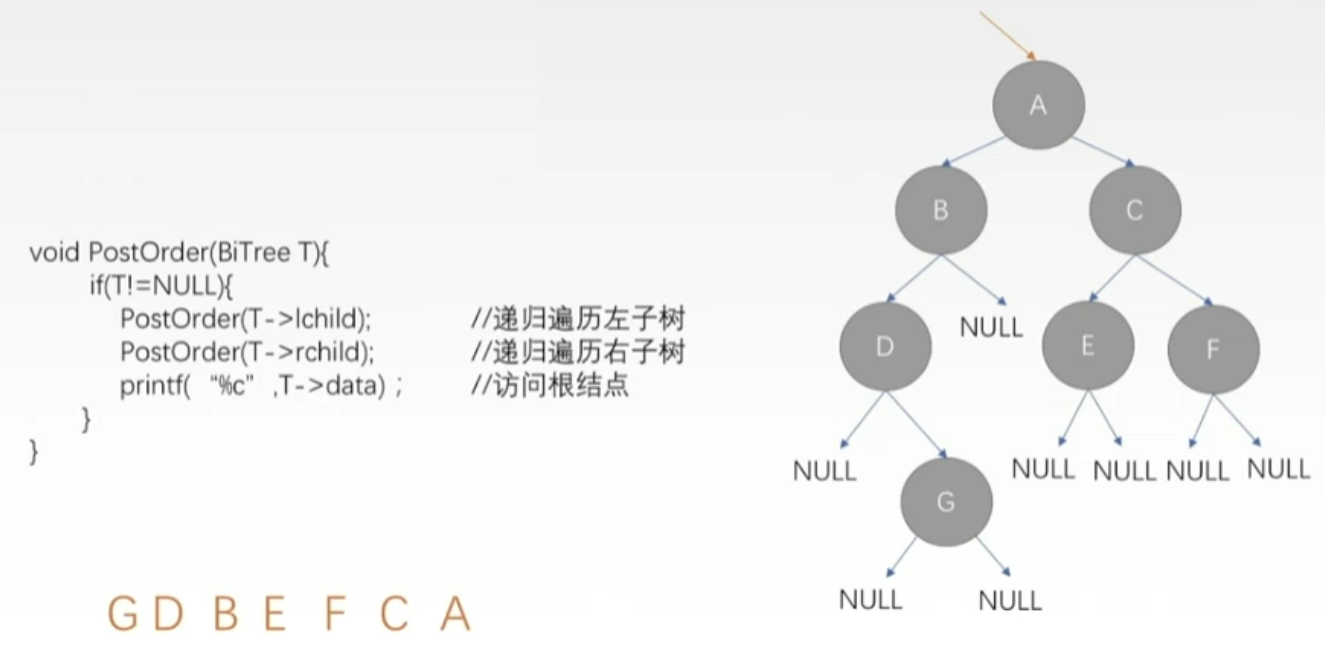
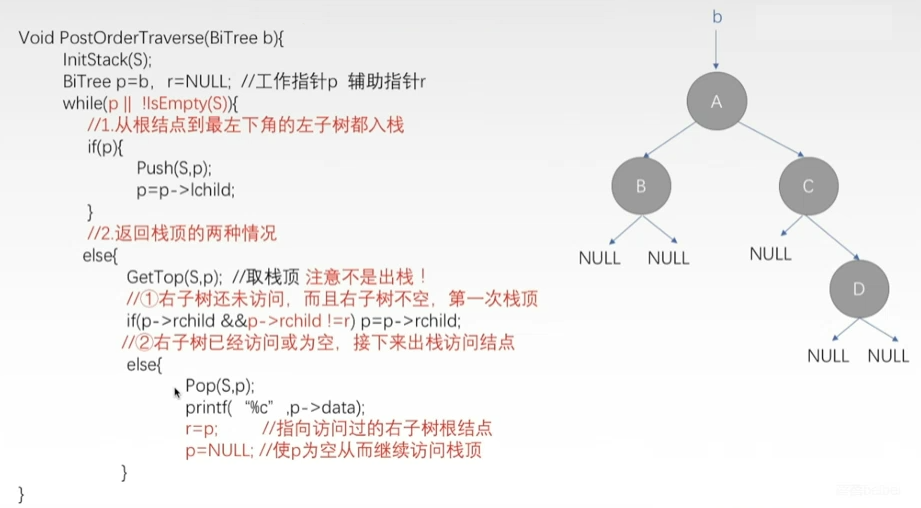
后序遍历
- 如果二叉树为空，什么也不做。否则：
  - 1）后序遍历左子树；
  - 2）后序遍历右子树
  - 3）访问根结点；
非递归先序遍历
非递归中序遍历
非递归后序遍历
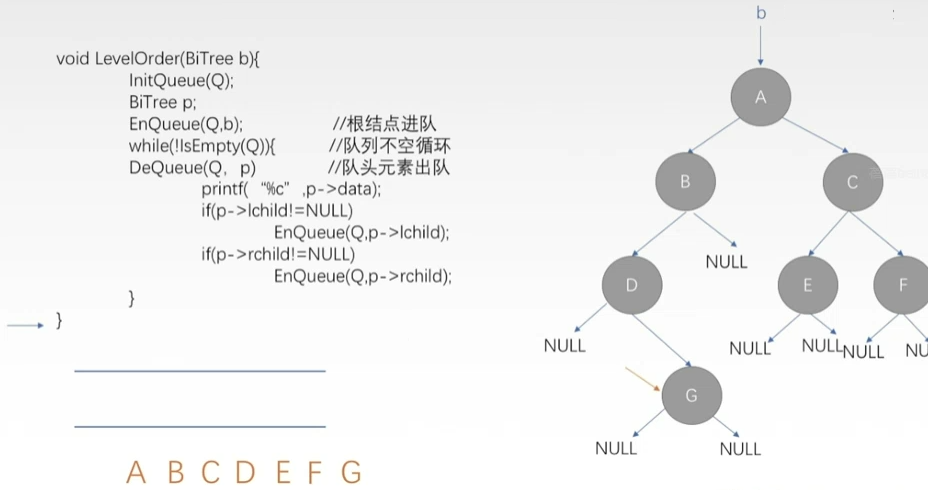
层序遍历
- 步骤
  - 若树为空，则什么都不做直接返回。
  - 否则从树的第一层开始访问，从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。
  - 访问完一个结点之后，把它的孩子存起来，而且先访问的结点，它的孩子也是先访问。
- 队列
  - 出队->访问->左右孩子入队

线索二叉树

二叉链表表示的二又树存在大量空指针
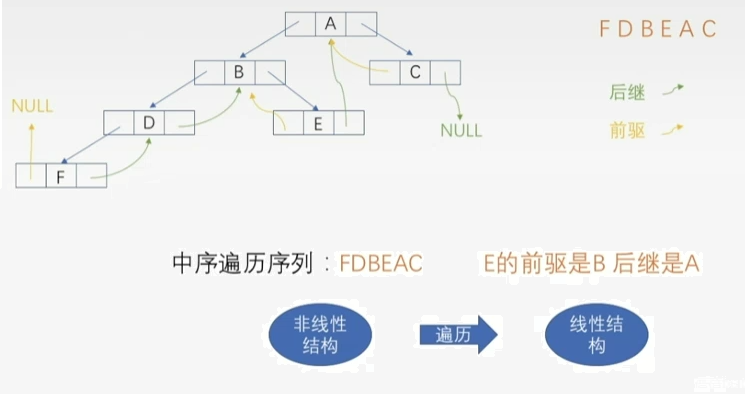
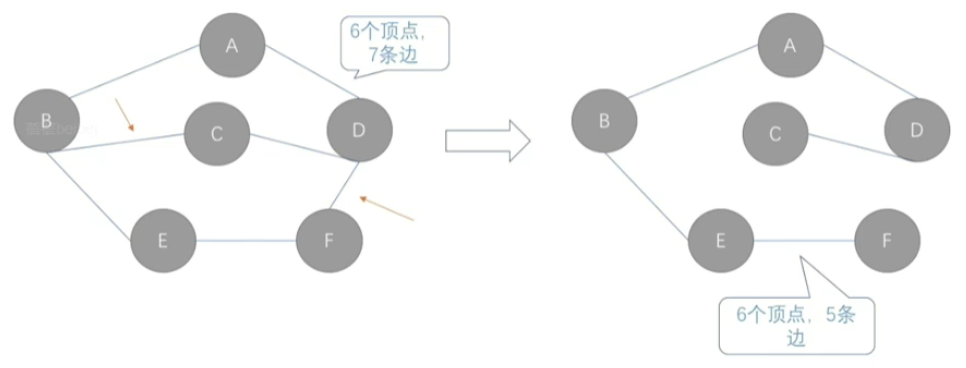
- N个结点的二叉链表，每个结点都有指向左右孩子的结点指针，所以一共有2N个指针，而N个结点的二叉树一共有N-1条分支，也就是说存在2N-（N-1)=N+1个空指针。比如下图二叉树中有6个结点，那么就有7个空指针。
指向前驱和后继的指针称为线索，加上线索的二叉链表就称为线索链表，相应的二叉树就称为线索二叉树
对二又树以某种次序遍历使其变为线索二又树的过程就叫做线索化
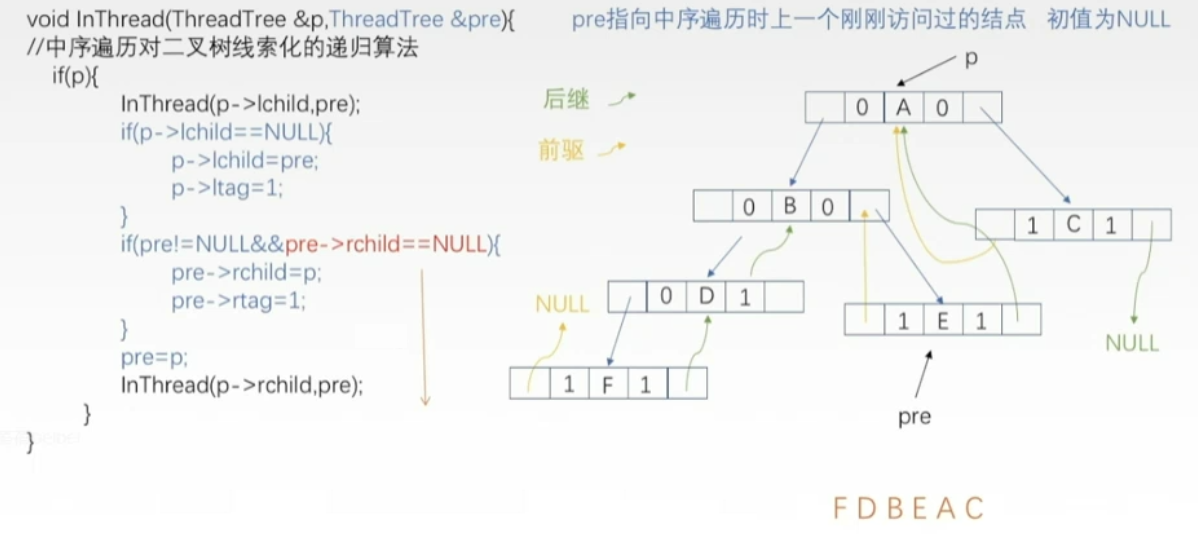
在二叉链表结点的结构基础上增加两个标志位Itag和rtag
- ltag == 0
  - lchild指向该结点左孩子
- ltag == 1
  - lchild指向该结点前驱
- rtag == 0
  - rchild指向该结点右孩子
- rtag == 1
  - rchild指向该结点后驱
中序遍历中前驱的右孩子如果为空，则访问完前驱下一个肯定访问该结点
构建

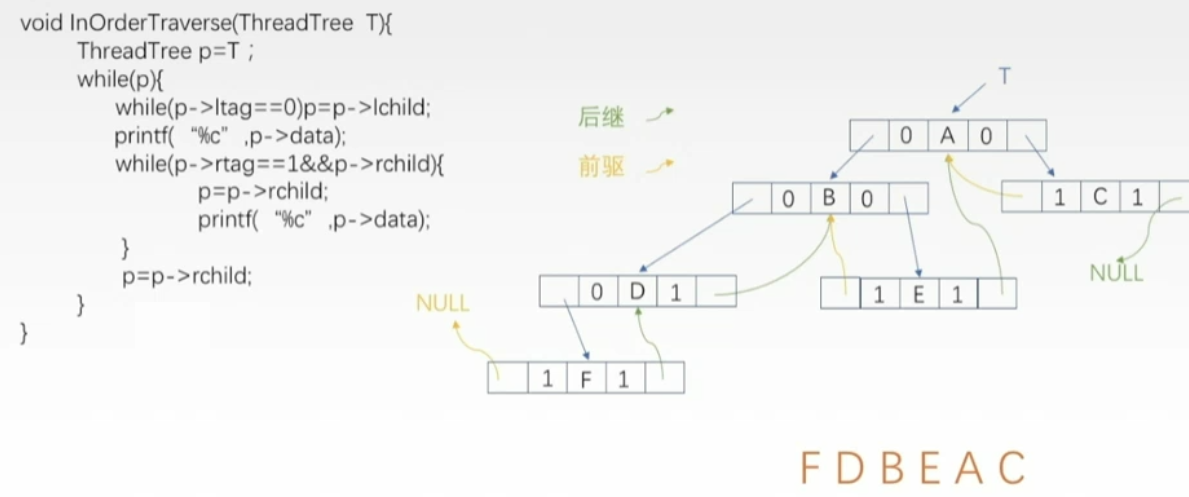
遍历

哈夫曼树和哈夫曼编码

权：树中结点相关的数值
路径长度：从树中某个结点到另一个结点之间的分支数目（经过的边数）
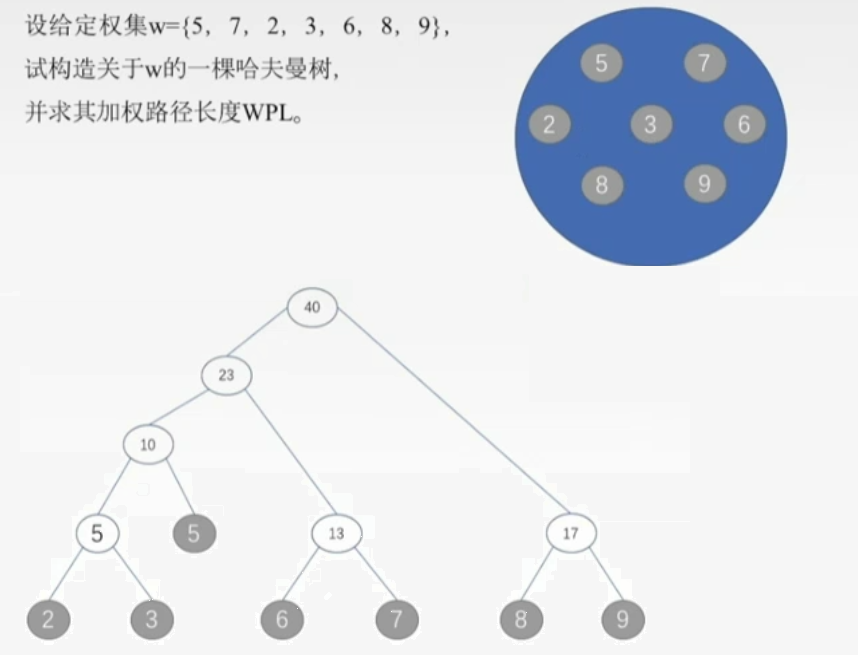
带权路径长度：从树的根结点到任意结点的路径长度（经过的边数）与该结点上权值的乘积称为该结点的带权路径长度
哈夫曼树：含有N个带权叶子结点的二叉树中，其中带权路径长度（WPL)最小的二叉树，也称为最优二叉树。
- 算法的描述如下：
  - 1）将这N个结点分别作为N棵仅含一个结点的二叉树，构成森林F（森林是m(m>= 0)颗互不相交的树的集合）。
  - 2)构造一个新结点，并从F中选取两棵根结点权值最小的树作为新结点的左、右子树，并且将新结点的权值置为左、右子树上根结点的权值之和。
    3）从F中删除刚才选出的两棵树，同时将新得到的树加入F中。
    4）重复步骤2)和3），直至F中只剩下一棵树为止。
1)每个初始结点最终都成为叶结点，并且权值越小的结点到根结点的路径长度越大。
2）构造过程中共新建了N-1个结点（双分支结点），因此哈夫曼树中结点总数为2N-1。
3）每次构造都选择2棵树作为新结点的孩子，因此哈夫曼树中不存在度为1的结点

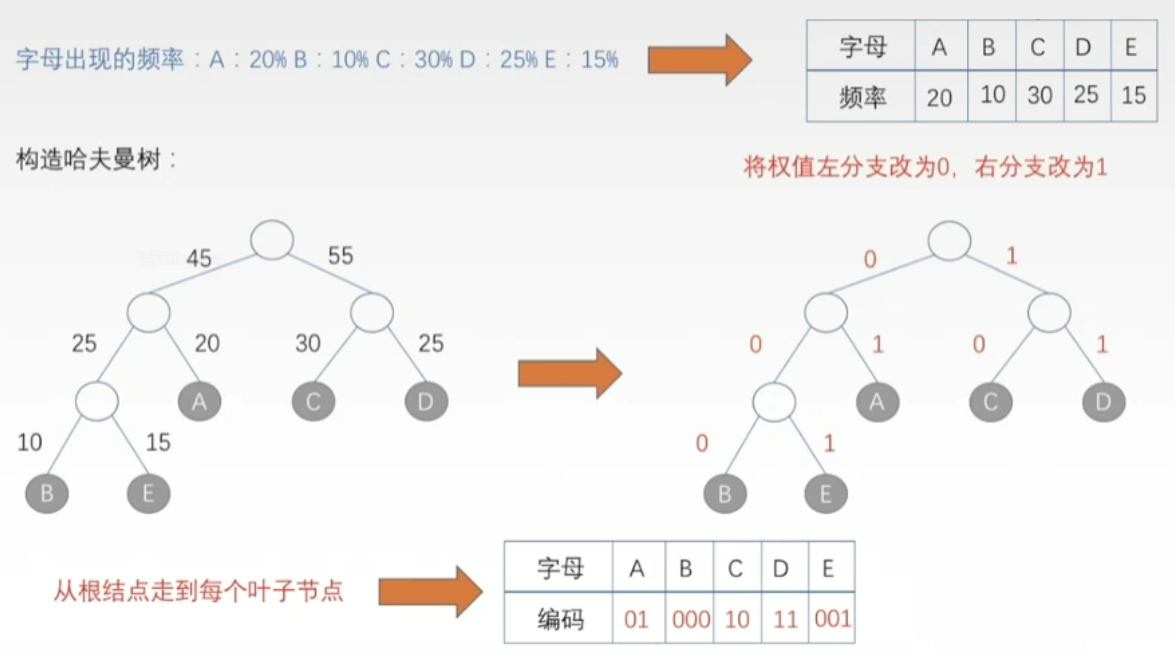
哈夫曼编码
哈夫曼编码最早用于解决远距离电报通信的数据传输最优化问题。
比如ABCDE这一段文字。通过网络传输要用到二进制的数字0和1。来保存A,B.C.D，E五个字母就可以了。

图

图G由顶点集V（Vertex）和边集E （Edge）组成，记为G=（V，E）
V（G)表示图G中顶点的有限非空集。
用|V|表示图G中顶点的个数，也称为图G的阶。
E（G）表示图中顶点之间的关系（边)集合。
用|E|表示图G中边的条数。
图不可为空，一个图中就算是一条边都没有，也就是边集为空，但是顶点集一定不为空。

有向图

有向边（弧）的有限集合

弧是顶点的有序对
<v，w>（注意是尖括号）
v是弧尾，w是弧头
v邻接到w或w临接自v

无向图

无向边（边）的有限集合
边是顶点的无序对
（v.w）（注意是圆括号）
（v,w） = (w,v)
w，v互为邻接点

简单图：
- 不存在顶点到自身的边
- 同一条边不重复出现
多重图：若图G中某两个结点之间的边数多于一条，又允许顶点通过同一条边和自己关联

完全图
- 无向完全图：如果任意两个顶点之间都存在边
  - 对于n个节点，每个顶点都与其他n-1个顶点有一条边，由于重复，所以一共有n*（n-1）/2条边
- 有向完全图：如果任意两个顶点之间都存在方向相反的两条弧
  - 对于n个节点，每个顶点都与其他n-1个顶点有一条边，由于有方向不重复，所以一共有**n*（n-1）**条边

图的基本概念

子图：设有两个图G=（V，E）和G’=（V’，E’)，若V’是V的子集，且E’是E的子集，则称G是G的子图。
若有满足V（G’）=V（G)的子图G’，则为G的生成子图
并非V和E的任何子集都能构成G的子图，因为这样的子集可能不是图，也就是说**，E的子集中的某些边关联的顶点可能不在这个V的子集中**。

连通: 顶点v到顶点v’有路径
- 连通图：图中任意两个顶点都是连通的
连通分量：无向图中的极大连通子图。
- 子图
- 连通
- 极大：①顶点足够多（比较性，和其他链条比最多的）②极大连通子图包含这些依附这些顶点的所有边
- 找连通分量的方法：
  - 从选取一个顶点开始，以这个顶点作为一个子图，然后逐个添加与这个子图相连的顶点和边直到所有相连的顶点都加入该子图
结论：如果一个图有n个顶点，并且有小于n-1条边，则此图必是非连通图。
强连通：
- 顶点v到顶点w和顶点w到顶点v都有路径
- 强连通图：图中任一对顶点都是强连通的
强连通分量：
- 有向图中的极大强连通子图。
- 子图
- 强连通
- 极大：①顶点足够多②极大强连通子图包含依附这些顶点的所有边

生成树
概念：包含图中全部n个顶点，但是只有n-1条边的极小连通子图
生成树去掉一条边则变成非连通图，加上一条边就会形成回路。
非连通图的生成森林：每个连通分量的生成树构成生成森林。

度
概念：以该顶点为一个端点的边数目
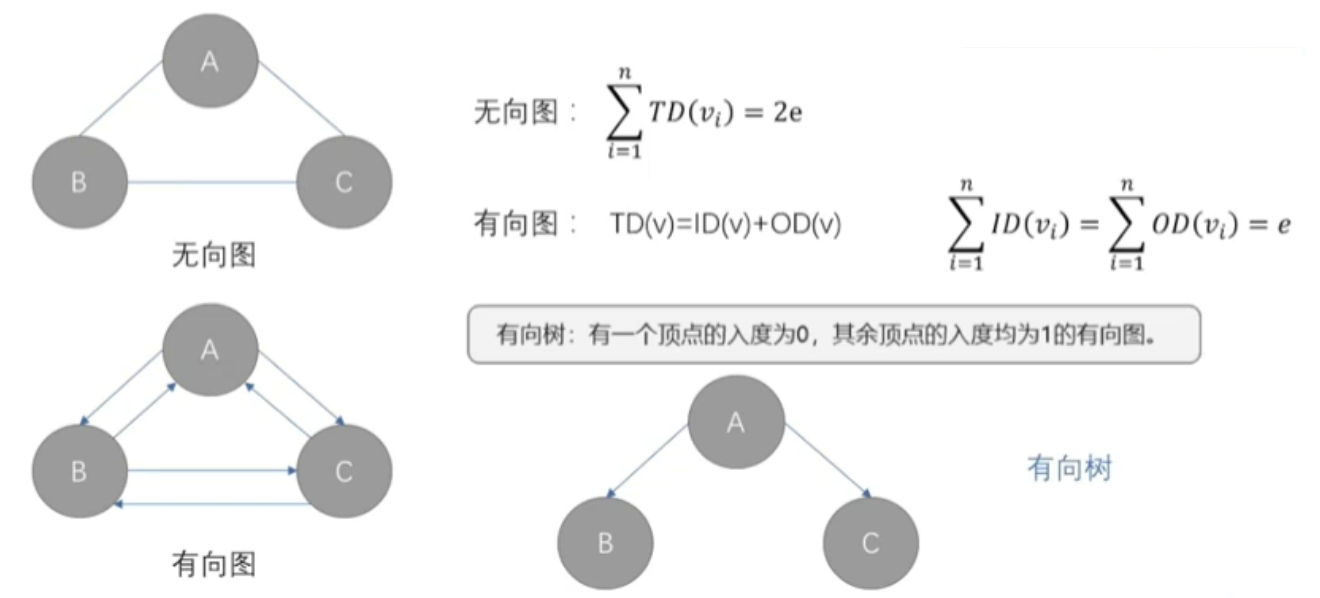
无向图中顶点v的度是指依附于该顶点的边的条数，记为TD（V)
有向图中顶点v的度分为出度和入度
- 入度（ID）In Degree是以顶点v为终点的有向边的数目
- 出度（OD)是以顶点v为起点的有向边的数目

权和网：
- 图中每条边可以赋予一定意义的数值，这个数值叫做这条边的权，有权值的图称为带权图，也叫做网
路径和路径长度：
- 顶点p到q之间的路径是指顶点序列p，a,b,c，d…q。路径上边的数目就是路径长度
回路（环）：
- 第一个和最后一个顶点相同的路径称为回路或者环。
简单路径和简单回路：
- 顶点不重复出现的路径称为简单路径。
- 对于回路，除了第一个和最后一个顶点其余顶点不重复出现的回路称为简单回路
距离：
- 从顶点u到v的最短路径长度。不存在路径则为无穷