了解二叉树的定义以及二叉树遍历之后,我们继续探讨二叉树的使用。二叉树是一种数据结构,是用来处理数据的。数据处理最简单的需求是查找、添加、删除,有一种二叉查找树可以满足以上需求。
二叉查找树也可以称之为有序二叉树。二叉查找树具有如下特性:
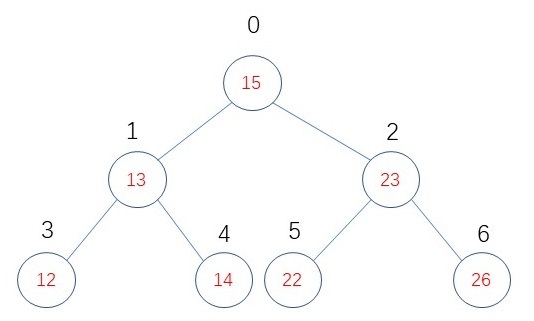
对于树中的每个节点n,其左子树中的值都小于节点n中的值,其右子树中的值都大于节点n中的值。
就像这样:
查找
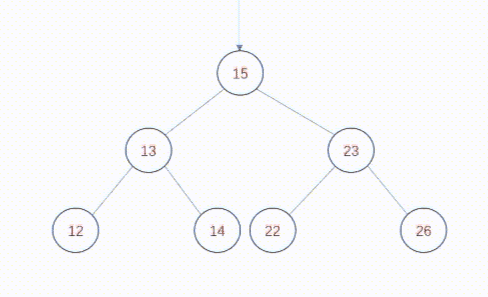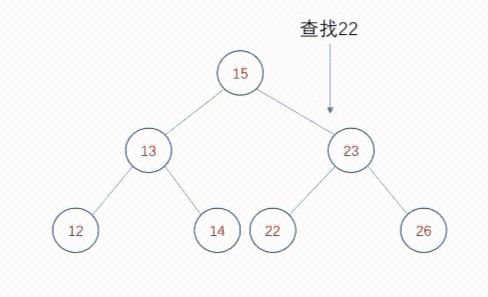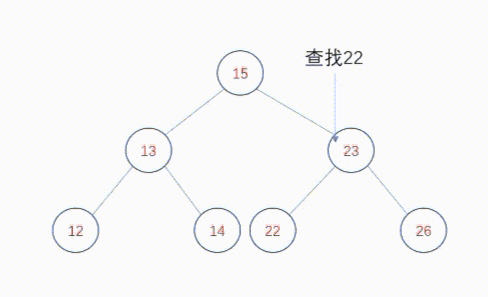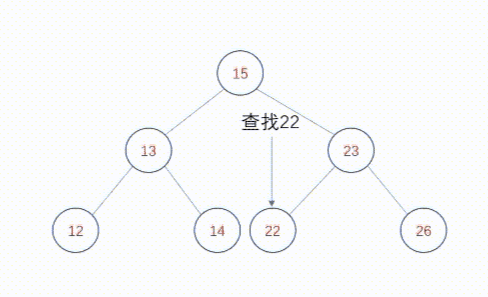
二叉查找树中查找某个元素的算法相当直观。对于每个节点,算法将要定位的值与当前所指节点中存储的值进行比较,如果该值小于存储值则转向左子树;如果该值大于存储值,则转向右子树。如果两者相同,很明显查找过程结束了。如果没有其他可以查找的节点,查找过程也终止,这表示该值不在树中。举个例子,在上图中查找22。从根节点开始,首先22大于根节点15,转向右子树,发现23大于查找节点22,随后转向左子树,发现22等于查找节点22,查找完毕。
动态图如下:
添加
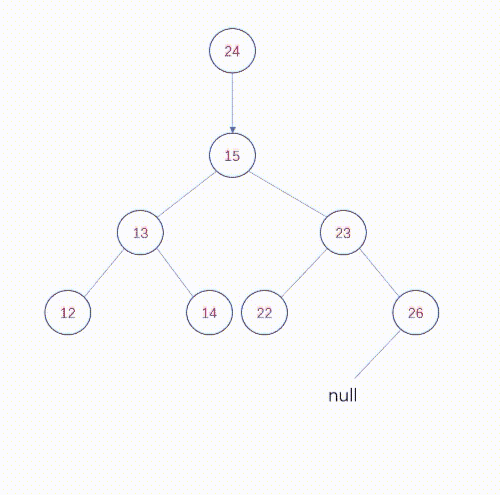
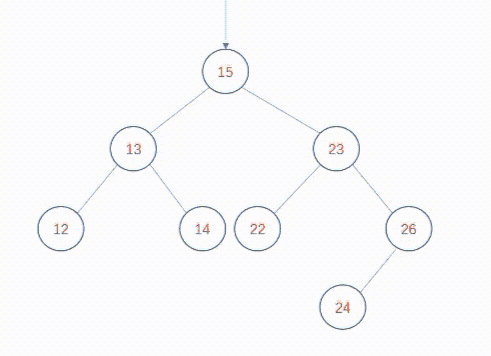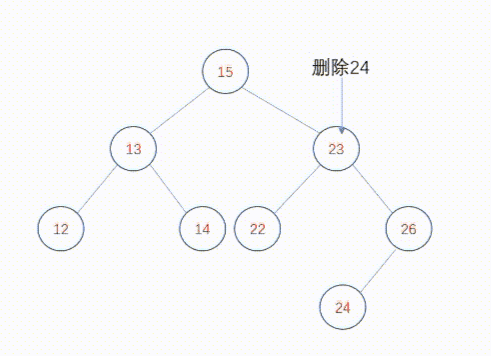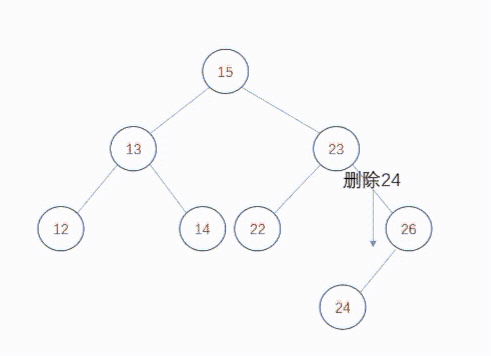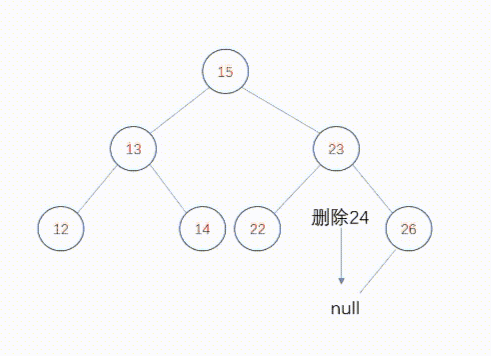
要插入键值为el的新节点,必须找到树中的一个终端节点,并将新节点与该节点连接。要找到这样一个终端节点,可以使用与查找树相同的技术:在扫描树的过程中,比较键值el与当前检查的节点的键值。如果el小于该键值,就测试当前节点的左子树,否则,就测试当前节点的右子树。如果要测试的p的子节点为空,就停止扫描,新节点将成为p的子节点。举个例子,在上图中插入24。从根节点开始,首先24大于根节点15,转向右子树,发现23小于插入节点24,转向右子树,发现26大于插入节点24,转向左子树,发现为空,将24添加为26节点的左子树,插入完毕。
动态图如下:
删除
另一个维护二叉查找树所必不可少的操作是删除节点。执行该操作的复杂度取决于要删除的节点在树中的位置。删除有两个子树的节点比删除叶子节点困难得多,删除算法的复杂度与被删除节点的子节点数目成正比。从二叉查找树中删除节点有三种情况:
1、删除叶节点
删除叶节点比较简单,因为叶节点没有子树,只要将父节点的相应指针设置为空即可。
动态图如下:
2、删除度为1的节点
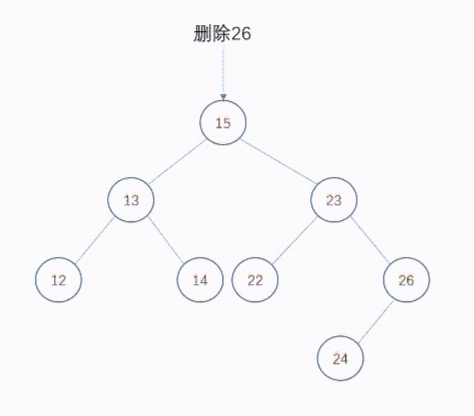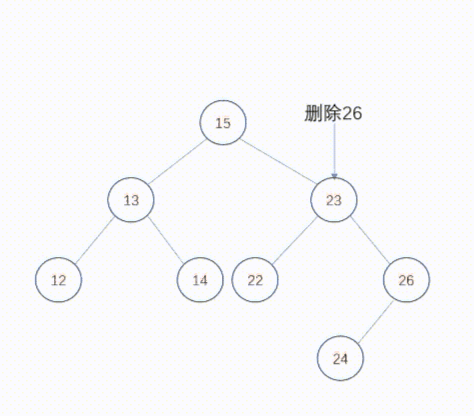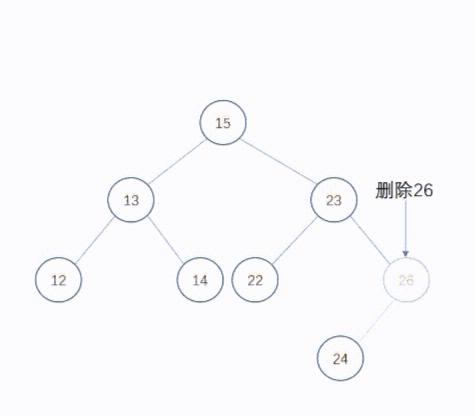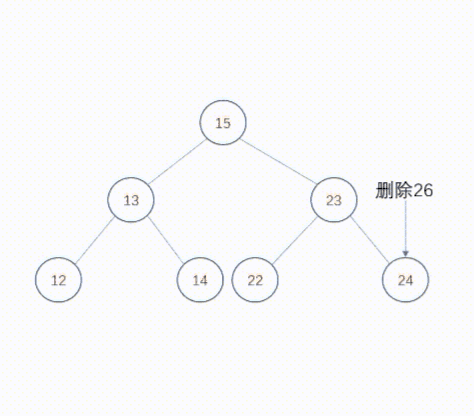
删除度为1的节点也不复杂,只要将父节点中指向该节点的指针重新设置为指向被删除节点的子节点。这样,被删除节点的子节点提升一个层次,其后的所有后裔节点根据家族关系依次提升一个层次。
动态图如下:
3、删除度2节点
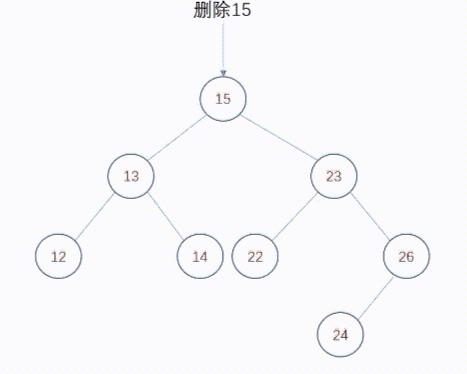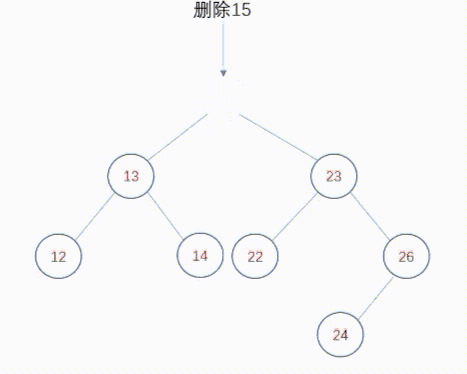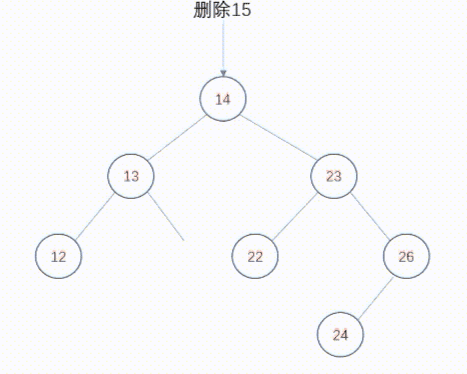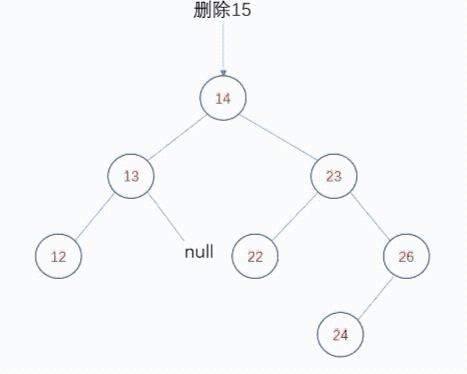
要删除的节点有两个子节点。在这种情况下,无法一步完成删除操作,因为父节点的右指针或者左指针不能同时指向被删除节点的两个子节点。下面讨论这一问题的两种不同解决方案。
合并删除
该解决方案从被删除节点的两颗子树中得到一棵树,然后将这颗树连接到被删除节点的父节点处。这种技术称为合并删除。但如何合并这些子树呢?根据二叉查找树的本质,右子树的每个值都比左子树的值大,所以最好的方法是找到左子树中具有最大值的节点,使它成为右子树的父节点。同样,还可以在右子树中找到具有最小值的节点,使之成为左子树的父节点。
动态图如下:
上图演示的是将右子树合并到左子树中成为一颗新的子树,然后将被删除节点的父节点重新指向子树。当然也可以将左子树合并到右子树,动态图如下:
删除有两个子树的节点比较麻烦,原因在于两个子树怎么处理?上面介绍的合并删除是一种解决方案,就是说将两颗子树合并成一颗新树,该树依然满足二叉查找树定义,然后将新树提升到删除节点的位置。合并删除关键逻辑是如何合并子树,如果我们决定将右子树挂在左子树上,那么挂在哪个节点比较合适呢?我们假设删除节点为p,p的左子树为m,右子树为n。那么,n中所有节点大于p,p大于m中所有节点。我们再假设m的根节点为m1,n的根节点为n1,那么n1比m中所有节点都大。也就是说,如果将n挂在m下,那么从m1到n1的路径中不能出现左指针,因为一旦出现左指针,就代表着n1成了一个 比它还小的节点的左子树,这就破坏了二叉查找树。因此,只要m1到n1的路径中没有左指针即可,最方便的做法就是使n1成为m树中最大节点的右子树。这正是上面动图中展示的内容。将左子树合并到右子树也是同理。看到这里,也许读者会产生一个疑问。假设m树中最大节点为m2,从m1到m2的路径中存在节点m3,那么使n1成为m3的右子树可以吗?这当然是可以的,但是如果这样做,就需要处理m3原有的右子树了。方法就是将m3原有右子树挂在n树上,要求是从n1到m3原有右子树根节点的路径中不能存在右指针,原理和上面类似。你会发现这样太麻烦了,应该直接将n树挂在m2下的,这样m2原来就没有右子树,所以就省去了后面的步骤。
合并删除是一种优秀的删除解决方案,但是它有一个缺陷,因为使用合并删除之后,会使二叉查找树的高度变大,经过多次的合并删除后,二叉查找树会退化为链表,这当然是不能容忍的。
为了规避合并删除的缺陷,还有一种叫做复制删除的解决方案。
复制删除
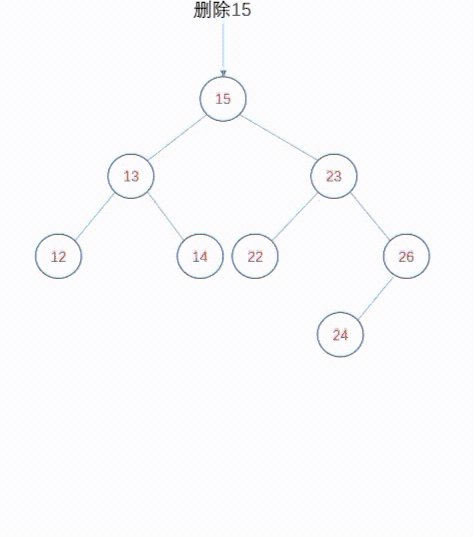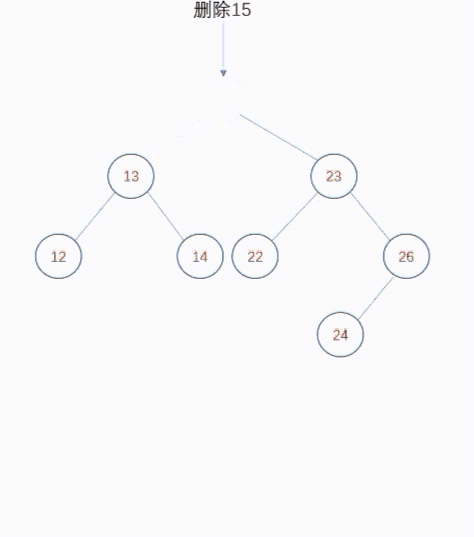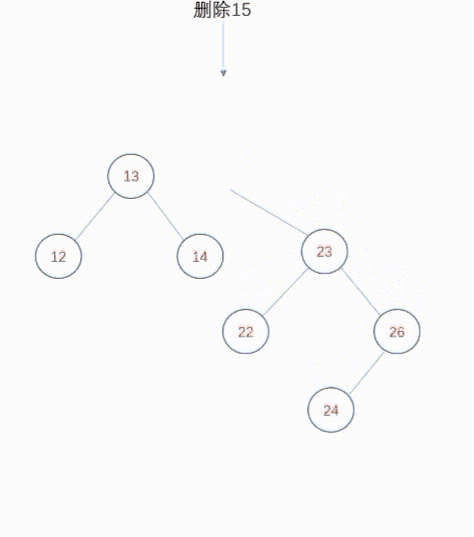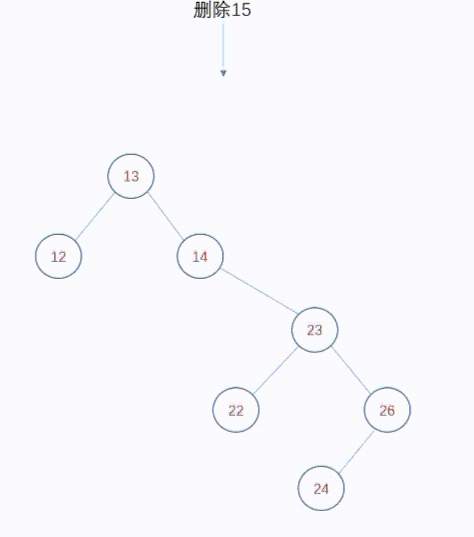
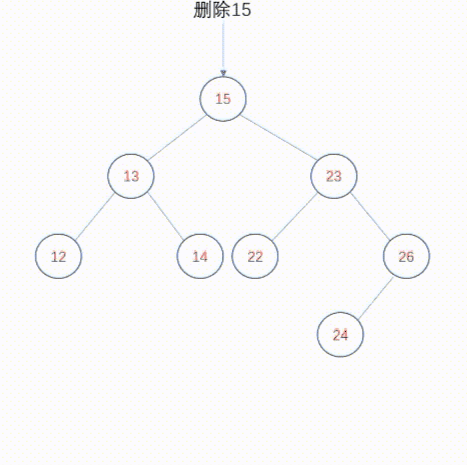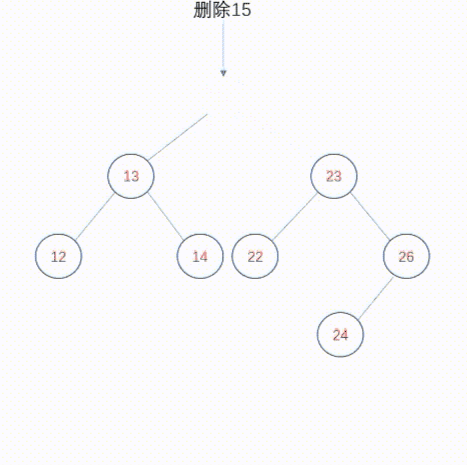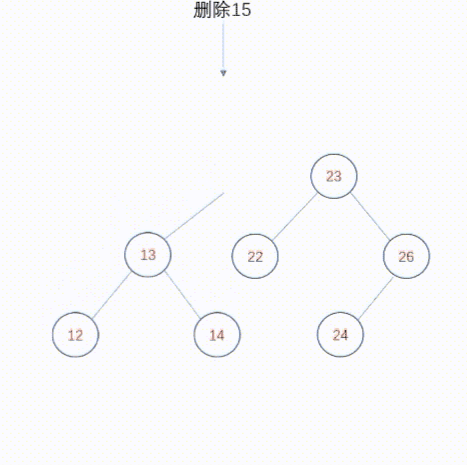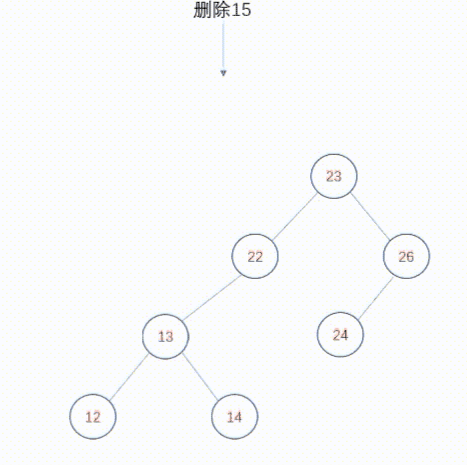
复制删除设计的非常巧妙。对于删除,我们直观的逻辑是删除某个节点,然后将该节点的子节点通过某种调整,然后提升到被删除节点的位置。复制删除不是这种逻辑,复制删除主张在被删除节点的两颗子树中,找到某个节点来替换被删除节点,这样就规避了提升子树的逻辑,并且不会破坏二叉查找树的高度。现在问题来了,被删除节点的两颗子树中,哪些节点可以用来替换被删除节点呢?答案就是被删除节点的直接前驱或者直接后继,直接前驱是其左子树中最右侧的节点(与此类似,其直接后继是右子树中最左侧的节点)。你会发现,直接前驱是左子树中最大的值,直接后继是右子树中最小的值,只有这两个节点可以替换被删除节点。你也许会问,为什么左右子树中其他节点不可以呢?因为如果找了其他节点p来替换被删除节点,那么就无法保证p大于左子树中所有节点,或者p小于右子树中所有节点,这就破坏了二叉查找树。因此,我们可以选择被删除节点的直接前驱或者直接后继来替换该节点,而我们知道,直接前驱或者直接后继要么是叶子节点,要么是只有一个子树。那么问题就变得简单了。使用直接前驱或者直接后继替换被删除节点之后,我们再把直接前驱或者直接后继删除掉,删除它们的逻辑比较简单,就是删除叶子节点或者删除度1节点,这在上面已经介绍过了。
动态图如下:
二叉查找树的查找、添加、删除逻辑到目前为止已经探讨完毕,更加深入的内容需要实践中摸索。下一节一起学习二叉树的平衡。
共同学习,写下你的评论
评论加载中...
作者其他优质文章