作者: david-yue
来源:CSDN
原文:https://blog.csdn.net/yueyihua/article/details/51027168
问题
这篇文章诞生的源头是我之前在stackoverflow看到的一个问题:
这个问题虽然国外的大神给出了完美的解释,但是我当时看过之后还是一头雾水。想必对x86架构上的cache没有较深入了解过的童鞋看过之后也是一样的感受吧。于是趁着寒假回家第一天还没有过多外界干扰的时候,我们就来详细的研究下x86架构下cache的组织方式吧。
我们就由这个问题开始讨论吧。这个问题说为什么转置一个512×512的矩阵反倒比513×513的矩阵要慢?(不知道什么是矩阵转置的童鞋补习线性代数去)提问者给出了测试的代码以及执行的时间。
不过我们不知道提问者测试机器的硬件架构,不过我的测试环境就是我这台笔记本了,x86架构,处理器是Intel Core i3-2310M 2.10GHz。顺便啰嗦一句,在linux下,直接用cat命令查看/proc/cpuinfo这个虚拟文件就可以查看到当前CPU的很多信息。
首先,我们将提问者给出的代码修改为C语言版,然后编译运行进行测试。提问者所给出的这段代码有逻辑问题,但是这和我们的讨论主题无关,所以请无视这些细节吧 :),代码如下:
#include <stdio.h>
#include <time.h>
#define SAMPLES 1000
#define MATSIZE 513
int mat[MATSIZE][MATSIZE];
void transpose()
{
int i, j, aux;
for (i = 0; i < MATSIZE; i++) {
for (j = 0; j < MATSIZE; j++) {
aux = mat[i][j];
mat[i][j] = mat[j][i];
mat[j][i] = aux;
}
}
}
int main(void)
{
int i, j;
for (i = 0; i < MATSIZE; i++) {
for (j = 0; j < MATSIZE; j++) {
mat[i][j] = i + j;
}
}
clock_t begin = clock();
for (i = 0; i < SAMPLES; i++) {
transpose();
}
clock_t elapsed = clock() - begin;
printf("Average for a matrix of %d : %f s\n",
MATSIZE, ((double)elapsed / CLOCKS_PER_SEC) / MATSIZE);
return 0;
}
我的机器上得出了如下的测试结果:
Average for a matrix of 513 : 0.003879 s
Average for a matrix of 512 : 0.004570 s
512×512的矩阵转置确实慢于513×513的矩阵,但是有意思的是我并没有提问者那么悬殊的执行结果。不过在编译命令行加上参数 -O2 优化后差异很明显了:
Average for a matrix of 513 : 0.001442 s
Average for a matrix of 512 : 0.005469 s
也就是说512×512的矩阵居然比513×513的矩阵转置平均慢了近4倍!
那么,是什么原因导致这个神奇的结果呢?
如果真是cache的缘故,那么cache又是如何影响代码执行的效率呢?
如果是因为cache具体的组织方式带来的特殊现象,那cache究竟是怎么组织的呢?
除此之外,仅仅是512×512的矩阵转置慢吗?其它的数字又会怎样呢?
搞明白了cache的组织方式之后,能给我们平时写代码定义变量有怎样的启示呢?
好了,我们提出的问题足够多了,现在我们来尝试在探索中逐一解答这些问题,并尝试分析一些现代CPU的特性对代码执行造成的影响。
cache原理
我们从cache的原理说起,cache存在的目的是在高速的CPU和较低速的主存储器之间建立一个数据存储的缓冲地带,通常由SRAM制造,访问速度略慢于CPU的寄存器,但是却高于DRAM制造的主存储器。因为制造成本过高,所以cache的容量一般都很小,一般只有几MB甚至几十到几百KB而已。那你可能会说,这么小的cache怎么可能有大作用。有趣的是还真有大作用,由于程序的局部性原理的存在,小容量的cache在工作时能轻易达到90%以上的读写命中率。局部性原理分为时间局部性和空间局部性,这里不再详述,有兴趣的童鞋请参阅其他资料。
顺便插一句嘴,不光金字塔型的存储器体系结构和制造成本相关,甚至我觉得计算机体系结构很大程度受制于成本等因素的考量。假设主存储器的存储速率能和CPU寄存器比肩的话,cache肯定就会退出历史的舞台了。如果磁盘的读写速度能达到寄存器级别并且随机存取,那恐怕内存也就没有存在的必要的……
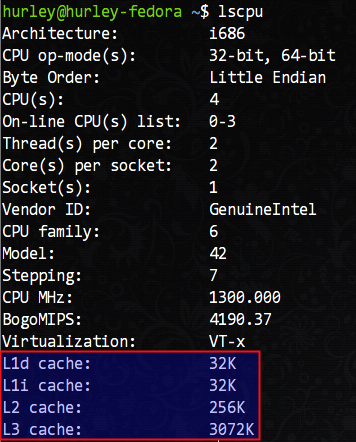
言归正传,我们如何查看自己机器(注:Linux机器 )上CPU的cache信息呢?/proc/cpuinfo这里是没有的,我们需要使用lscpu命令查看,这条命令在我的机器上得到了如下的输出结果:
可以看到,我的机器拥有L1d(L1数据cache)和L1i(L1指令cache)各32KB、L2 cache 256KB、L3 cache 3072KB(3MB)。
L1缓存居然分为数据缓存和指令缓存,这不是哈佛架构么?x86不是冯·诺伊曼架构么,怎么会在存储区域区分指令和数据?其实,教科书中讲述的都是完全理想化的模型,在实际的工程中,很难找到这种理想化的设计。就拿操作系统内核而言,尽管所谓的微内核组织结构更好,但是在目前所有知名的操作系统中是找不到完全符合学术意义上的微内核的例子。工程上某些时候就是一种折衷,选择更“接地气”的做法,而不是一味的契合理论模型。
既然cache容量很有限,那么如何组织数据便是重点了。接下来,我们谈谈cache和内存数据的映射方式。一般而言,有所谓的全相联映射,直接相联映射和组相联映射三种方式。
CPU和cache是以字为单位进行数据交换的,而cache却是以行(块)(即Cache Block,或Cache Line)为单位进行数据交换的。在cache中划分若干个字为一行,在内存中划分若干个字为一块,这里的行和块是大小相等的。CPU要获取某内存地址的数据时会先检查该地址所在的块是否在cache中,如果在称之为cache命中,CPU很快就可以读取到所需数据;反之称为cache未命中,此时需要从内存读取数据,同时会将该地址所在的整个内存块复制到cache里存储以备再次使用。
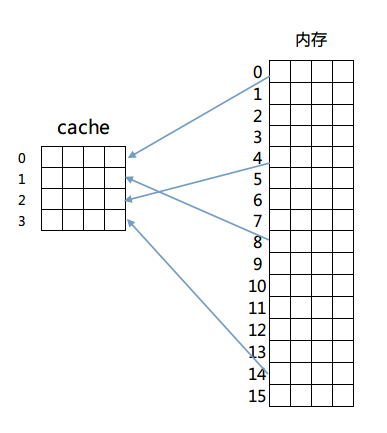
我们依次来看这三种映射方式,首先是全相联映射,这种映射方式很简单,内存中的任意一块都可以放置到cache中的任意一行去。为了便于说明,我们给出以下的简单模型来理解这个设计。
我们假设有一个4行的cache,每行4个字,每个字占4个字节,即64字节的容量。另外还有256字节(16块,每块4字,每字4字节)的一个RAM存储器来和这个cache进行映射。映射结构如图所示:
那么如何判断cache是否命中呢?由于内存和cache是多对一的映射,所以必须在cache存储一行数据的同时标示出这些数据在内存中的确切位置。简单的说,在cache每一行中都有一个Index,这个Index记录着该行数据来自内存的哪一块(其实还有若干标志位,包括有效位(valid bit)、脏位(dirty bit)、使用位(use bit)等。这些位在保证正确性、排除冲突、优化性能等方面起着重要作用)。那么在进行一个地址的判断时,采用全相联方式的话,因为任意一行都有可能存在所需数据,所以需要比较每一行的索引值才能确定cache中是否存在所需数据。这样的电路延迟较长,设计困难且复杂性高,所以一般只有在特殊场合,比如cache很小时才会使用。
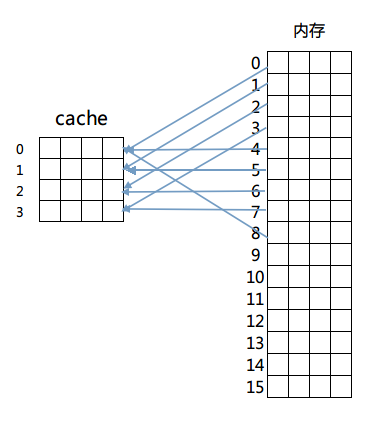
然后是第二种方法:直接相连映射。这个方法固定了行和块的对应关系,例如内存第0块必须放在cache第0行,第一块必须放在第一行,第二块必须放在第二行……循环放置,即满足公式:
内存块放置行号 = 内存块号 % cache总行数
映射如图所示:
这样做解决了比较起来困难的问题,由于每一块固定到了某一行,只需要计算出目标内存所在的行号进行检查即可判断出cache是否命中。但是这么做的话因为一旦发生冲突就必须换出cache中的指定行,频繁的更换缓存内容造成了大量延迟,而且未能有效利用程序运行期所具有的时间局部性。
综上,最终的解决方案是最后的组相联映射方式(Set Associativity),这个方案结合了以上两种映射方式的优点。具体的方法是先将cache的行进行分组,然后内存块按照组号求模来决定该内存块放置到cache的哪一个组。但是具体放置在组内哪一行都可以,具体由cache替换算法决定。
我们依旧以上面的例子来说明,将cache里的4行分为两组,然后采用内存里的块号对组号求模的方式进行组号判断,即内存0号块第一组里,2号块放置在第二组里,3号块又放置在第一组,以此类推。这么做的话,在组内发生冲突的话,可以选择换出组内一个不经常读写的内存块,从而减少冲突,更好的利用了资源(具体的cache替换策略不在讨论范围内,有兴趣的童鞋请自行研究)。同时因为组内行数不会很多,也避免了电路延迟和设计的复杂性。
x86中cache的组织方式采用的便是组相联映射方式。
上面的阐述可能过于简单,不过大家应该理解了组相联映射方式是怎么回事了。那么我们接下来结合我的机器上具体的cache映射计算方法继续分析。
我们刚说过组相联映射方式的行号可以通过 块号 % 分组个数 的公式来计算,那么直接给出一个内存地址的话如何计算呢?其实内存地址所在的块号就是 内存地址值 / 分块字节数,那么直接由一个内存地址计算出所在cache中的行分组的组号计算公式就是:
内存地址所在cache组号 = (内存地址值 / 分块字节数) % 分组个数
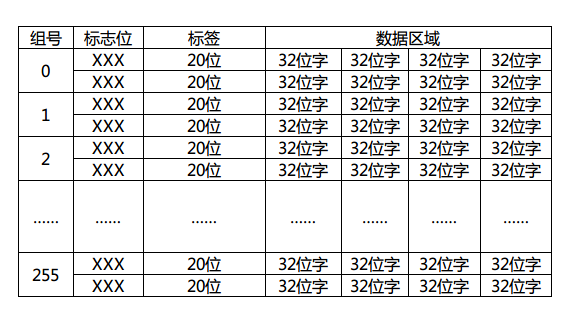
很简单吧?假定一个cache行(内存块)有4个字,我们画出一个32位地址拆分后的样子:
因为字长32的话,每个字有4个字节,所以需要内存地址最低2位时字节偏移,同理每行(块)有4个字,块内偏移也是2位。这里的索引位数取决于cache里的行数,这个图里我画了8位,那就表示cache一共有256个分组(0~255)存在,每个分组有多少行呢?这个随意了,这里的行数是N,cache就是N路组相联映射。具体的判断自然是取tag进行组内逐一匹配测试了,如果不幸没有命中,那就需要按照cache替换算法换出组内的一行了。顺带画出这个地址对应的cache结构图:
标志位是有效位(valid bit)、脏位(dirty bit)、使用位(use bit)等,用于该cache行的写回算法,替换算法使用。这里简单期间我就画了一个2路组相联映射的例子出来。现在大家应该大致明白cache工作的流程了吧?首先由给出的内存地址计算出所在cache的组号(索引),再由判断电路逐一比较标签(tag)值来判断是否命中,若命中则通过行(块)内偏移返回所在字数据,否则由cache替换算法决定换出某一行(块),同时由内存调出该行(块)数据进行替换。
其实工作的流程就是这样,至于cache写回的策略(写回法,写一次法,全写法)不在本文的讨论范围之内,就不细说了。
有了以上铺垫,我们终于可以来解释那个512×512的矩阵转置问题了。很艰难的铺垫,不是吗?但我们距离胜利越来越近了。
512×512的矩阵,或者用C语言的说法称之为512×512的整型二维数组,在内存中是按顺序存储的。
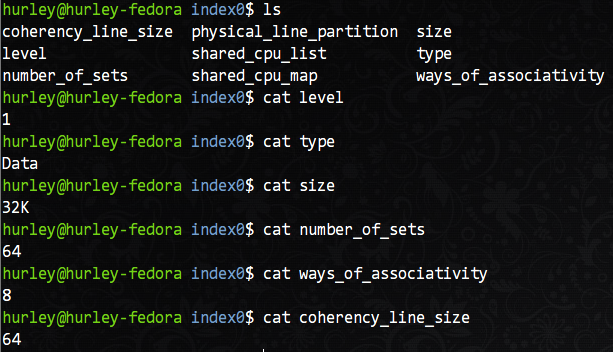
那么以我的机器为例,在上面的lscpu命令输出的结果中,L1d(一级数据缓存)拥有32KB的容量。但是,有没有更详细的行大小和分组数量的信息?当然有,而且不需要多余的命令。在/sys/devices/system/cpu目录下就可以看到各个CPU核的所有详细信息,当然也包括cache的详细信息,我们主要关注L1d缓存的信息,以核0为例,在/sys/devices/system/cpu/cpu0/cache目录下有index0~index4这四个目录,分别对应L1d,L1i,L2,L3的信息。我们以L1d(index0)为例查看详细参数。
从图中我们可以知道,这是L1数据缓存的相关信息:共有64个组,每组8行,每行16字(64字节),共有32KB的总容量。按照我们之前的分析,相信你很容易就能说出这个机器上L1d缓存的组织方式。没错,就是8路组相联映射。
顺带贴出Intel的官方文档证明我不是在信口开河:
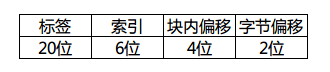
此时32位内存地址的拆分如下:
对应的cache图想必也难不倒大家吧?和上边的cache结构不同的就是改变了分组数量、每组行数和每行大小。
我们继续分析转置问题。每个cache行(块)拥有64个字节,正好是16个int变量的大小。一个n阶矩阵的一个行正好填充n / 16个cache行。512阶矩阵的话,每个矩阵的行就填充了32个组中的行,2个矩阵的行就覆盖了64个组。之后的行若要使用,就必然牵扯到cache的替换了。如果此时二维数组的 array[0][0] 开始从cache第一行开始放置。那么当进入第二重for循环之后,由于内存地址计算出的cache组号相同,导致每一个组中的正在使用的cache行发生了替换,不断发生的组内替换使得cache完全没有发挥出效果,所以造成了512×512的矩阵在转置的时候耗时较大的原因。具体的替换点大家可以自行去计算,另外513×513矩阵大家也可以试着去分析没有过多cache失效的原因。不过这个问题是和CPU架构有关的,所以假如你的机器没有产生同样的效果,不妨自己研究研究自己机器的cache结构。
另外网上针对这个问题也有诸多大牛给出的解释,大家不妨参照着理解吧。别人说过的我就不说了,大家可以参考着分析。
原本想把这篇作为上篇,再去写一个下篇讲述一些编程中要注意的问题。不过偶然间看到了微软大牛Igor Ostrovsky的博文《Gallery of Processor Cache Effects》,瞬间感觉自己不可能写的更好了。所以推荐大家去读这篇文章。如果感觉英文吃力的话,耗子叔这里有@我的上铺叫路遥做的翻译解释《7个示例科普CPU Cache》。
另外,开源中国这里的一篇译文也有参考价值:每个程序员都应该了解的 CPU 高速缓存》。
共同学习,写下你的评论
评论加载中...
作者其他优质文章