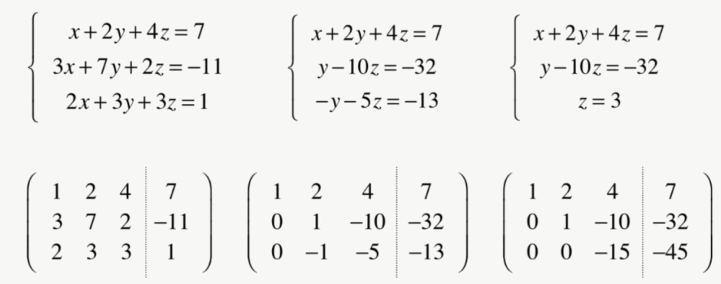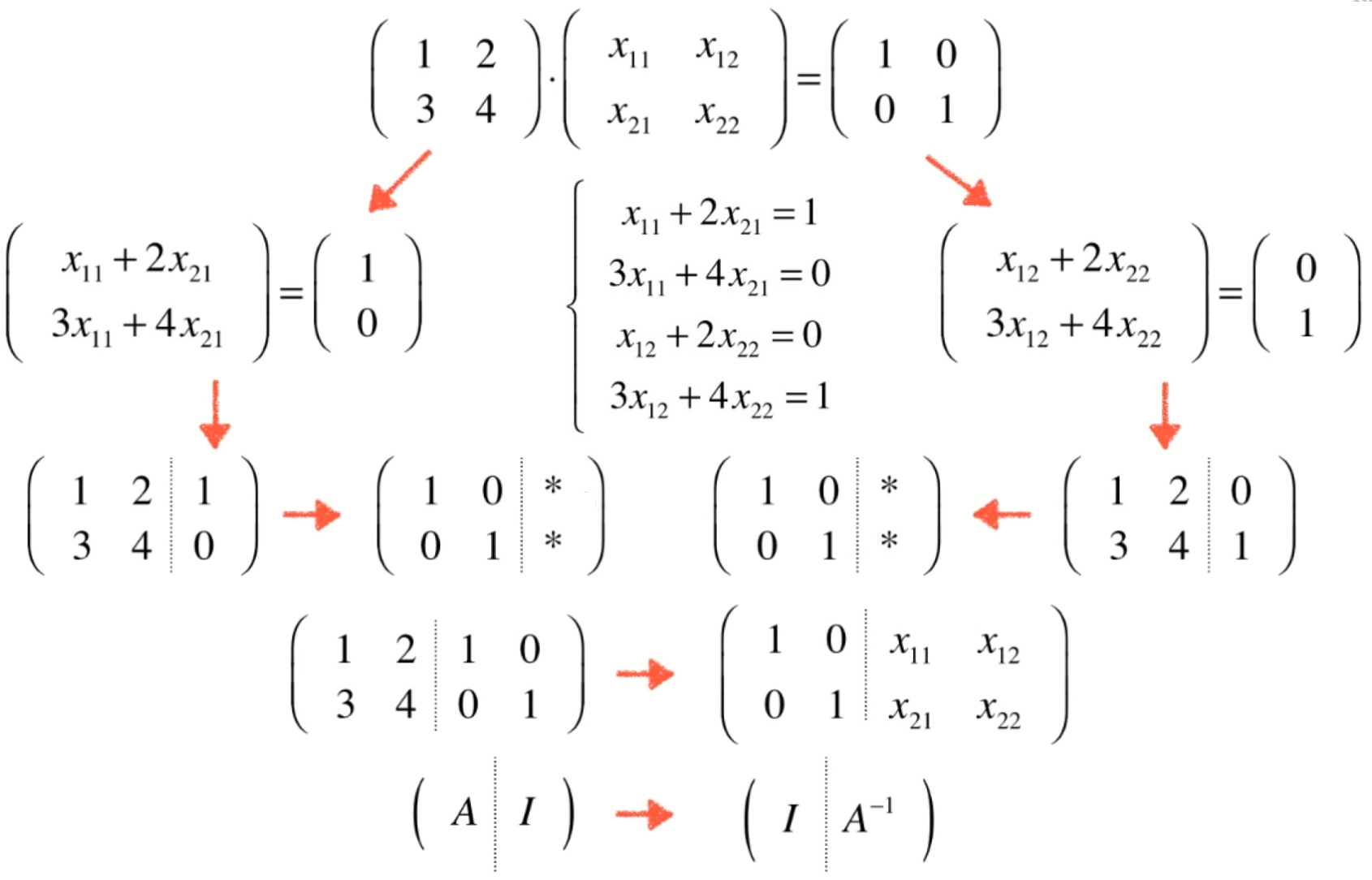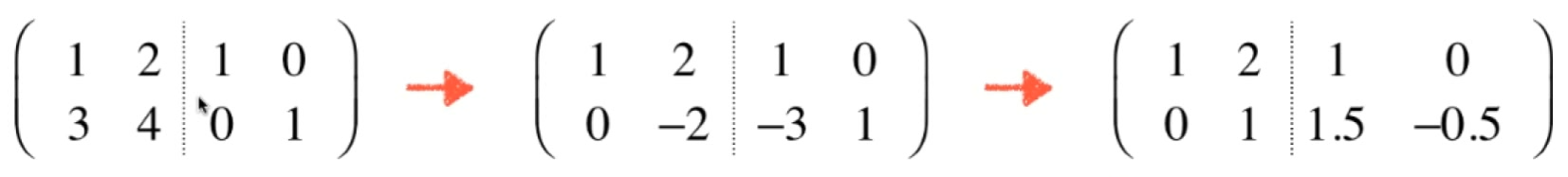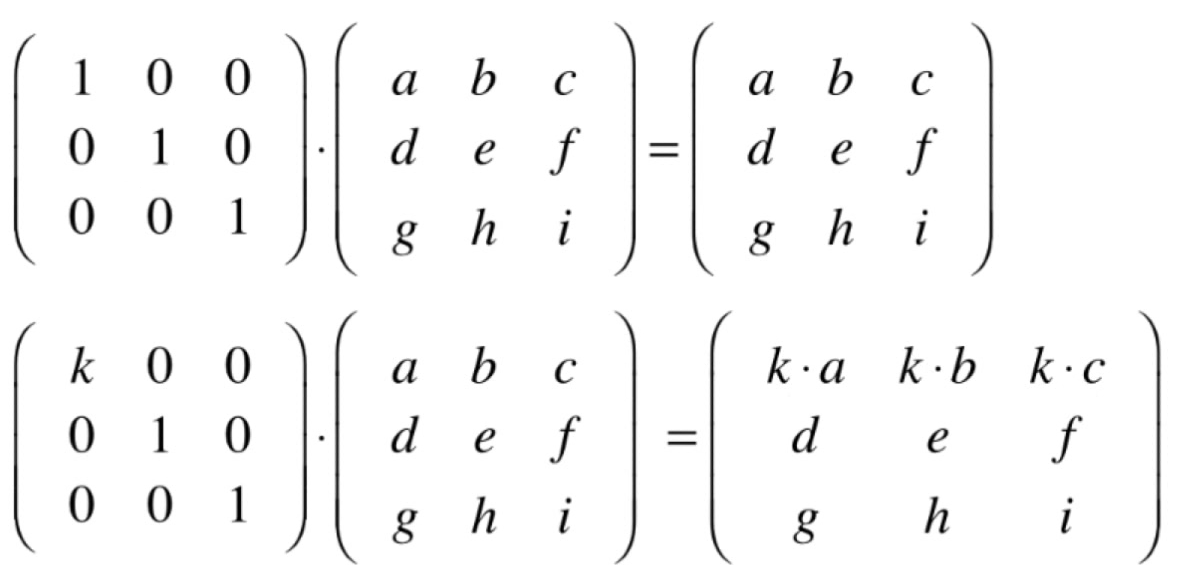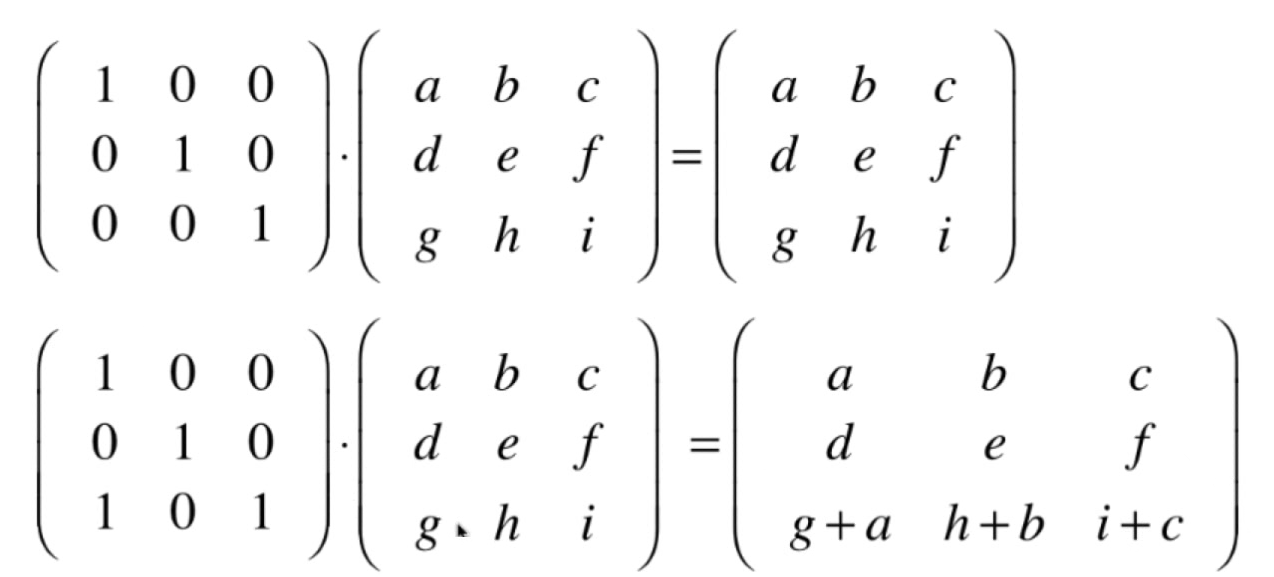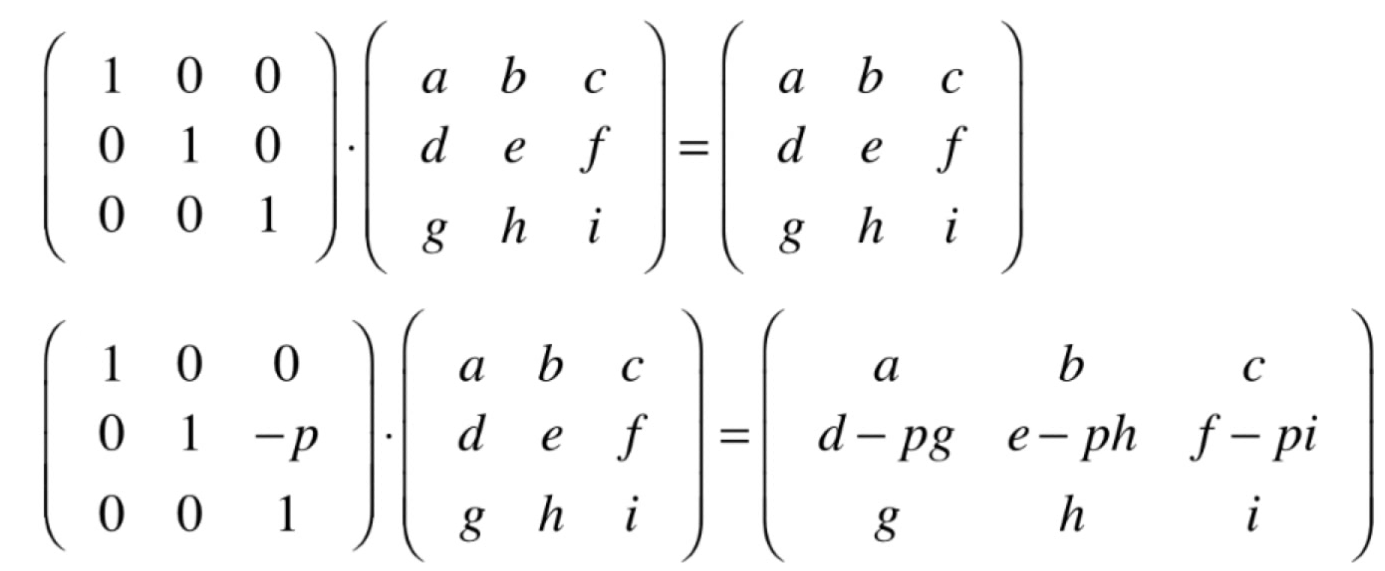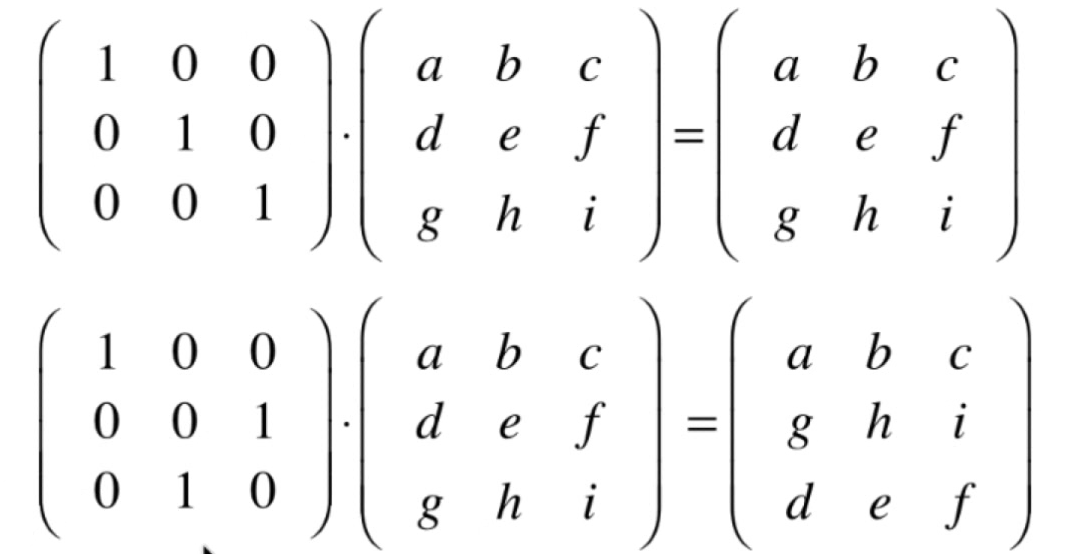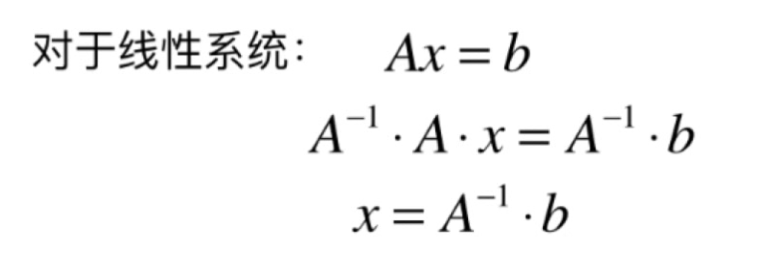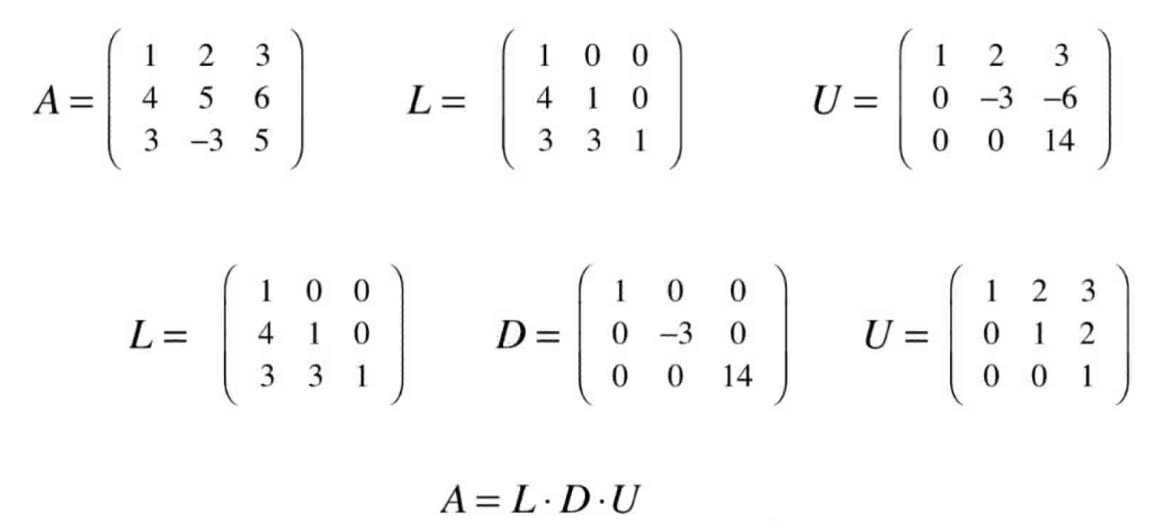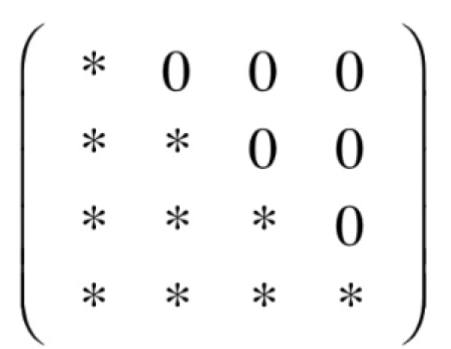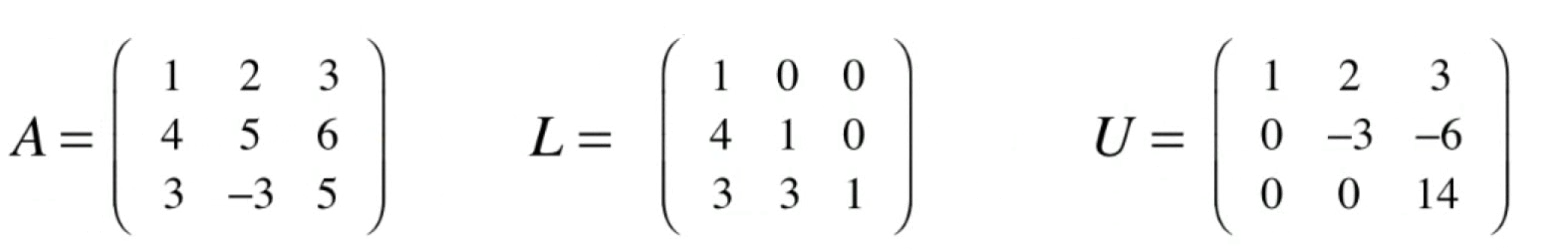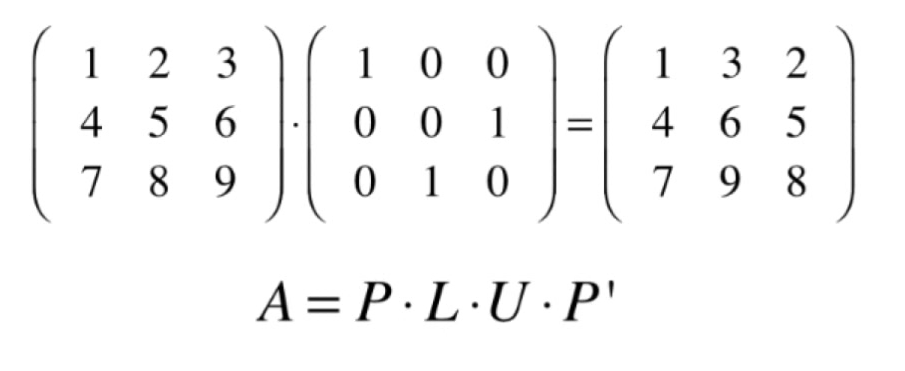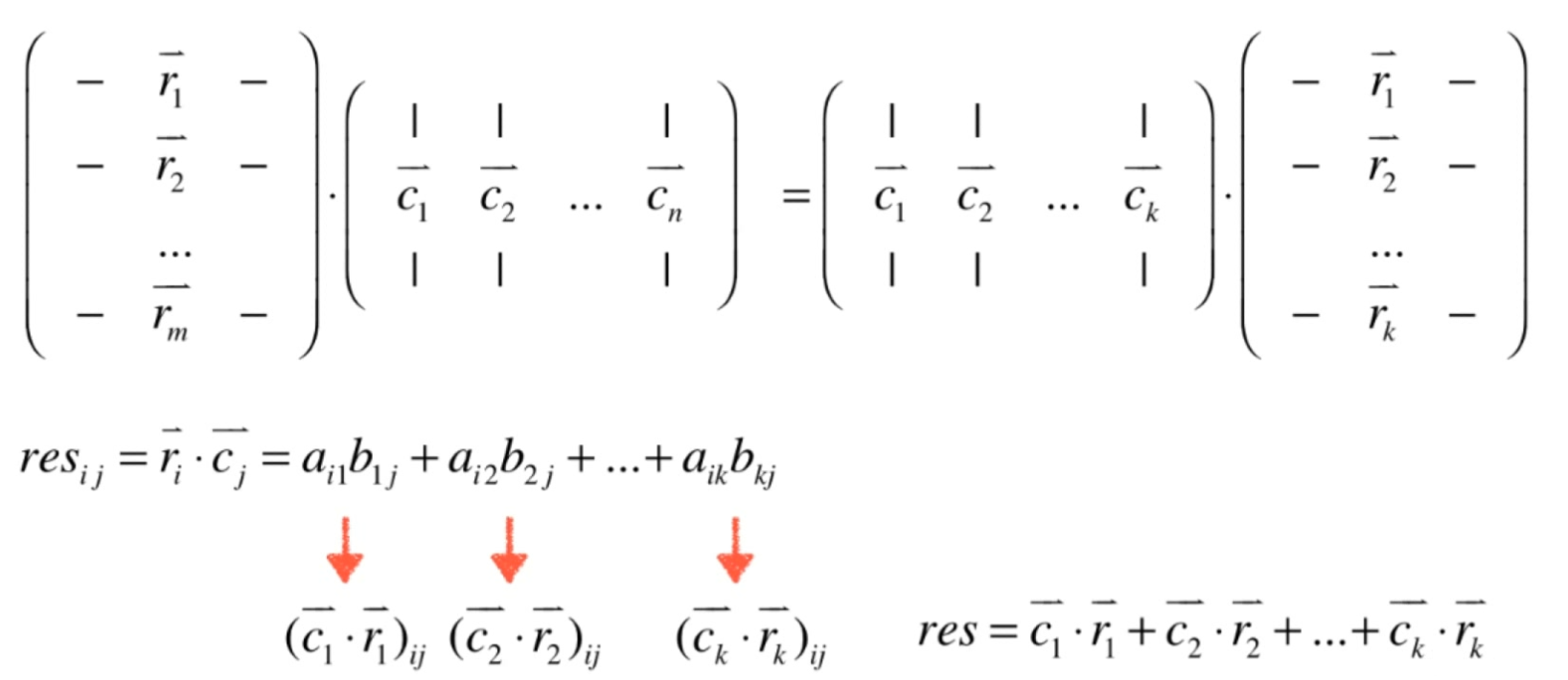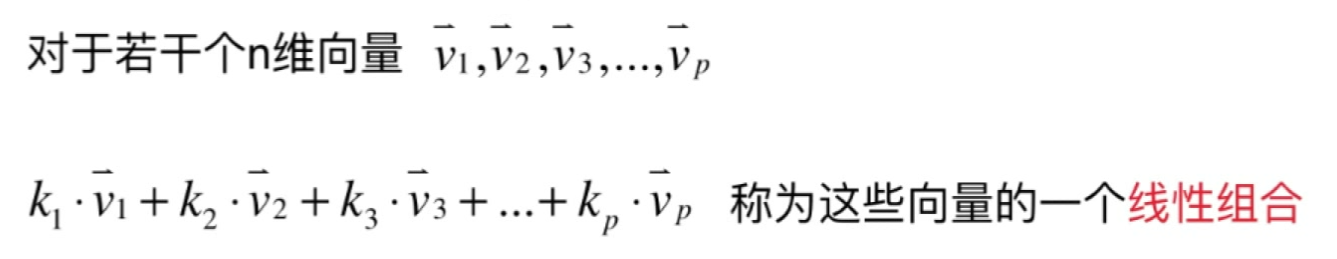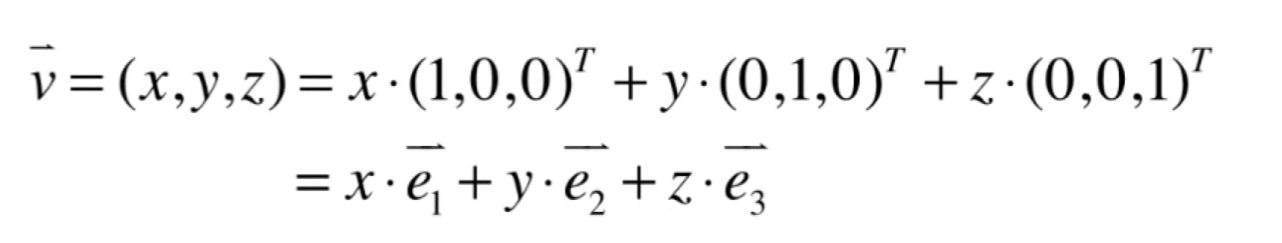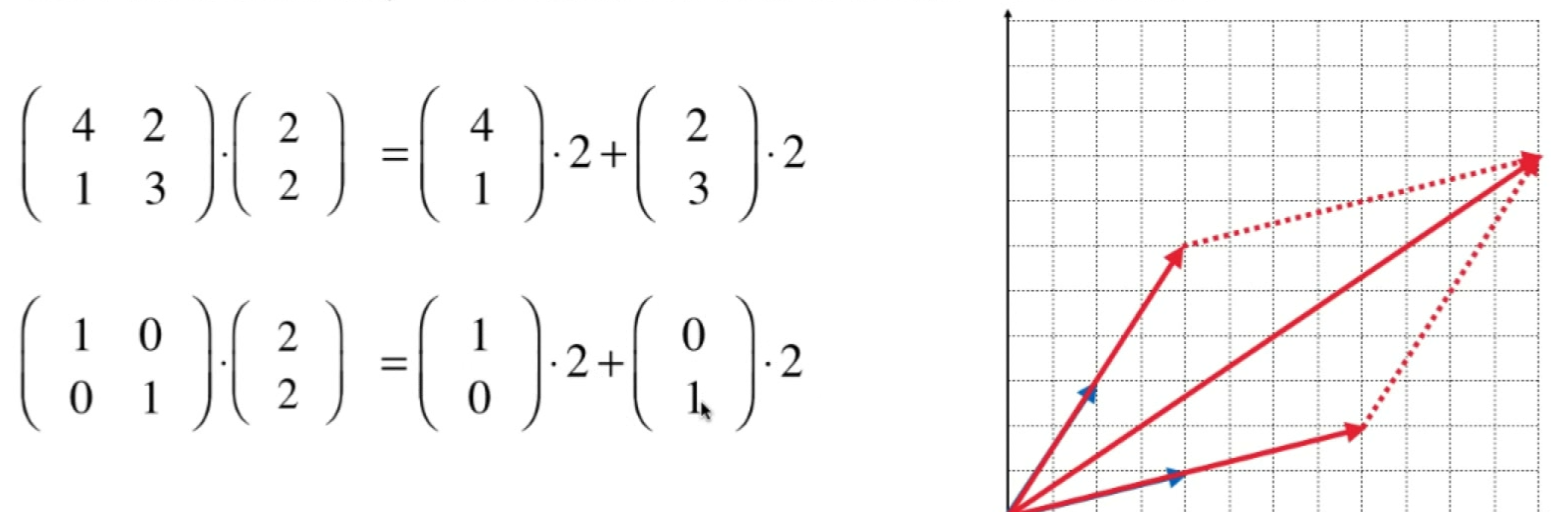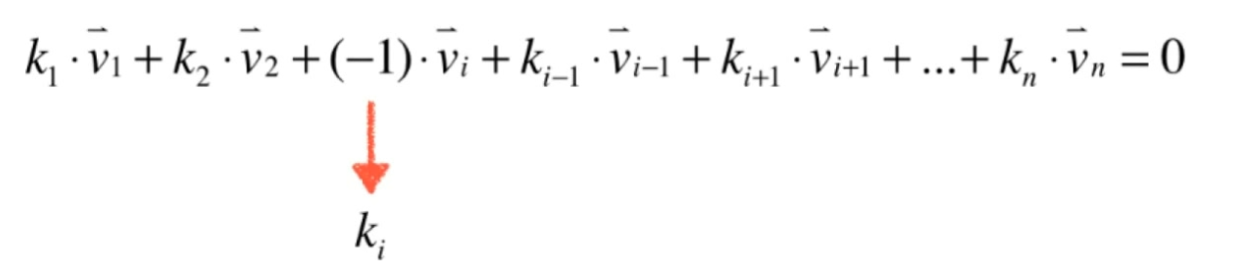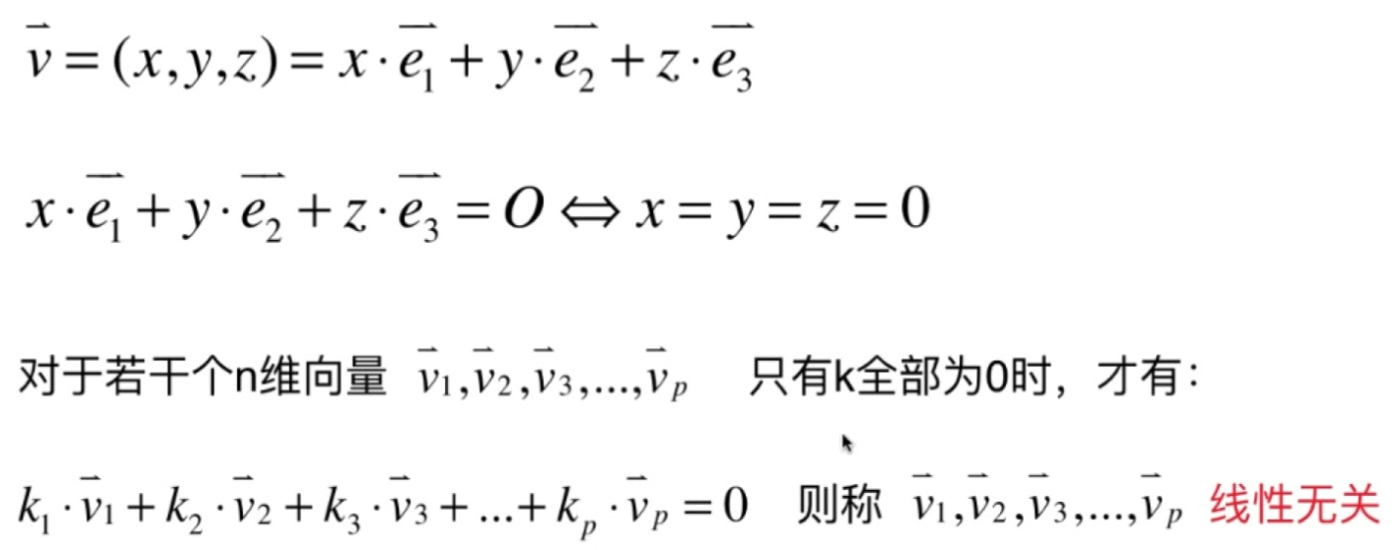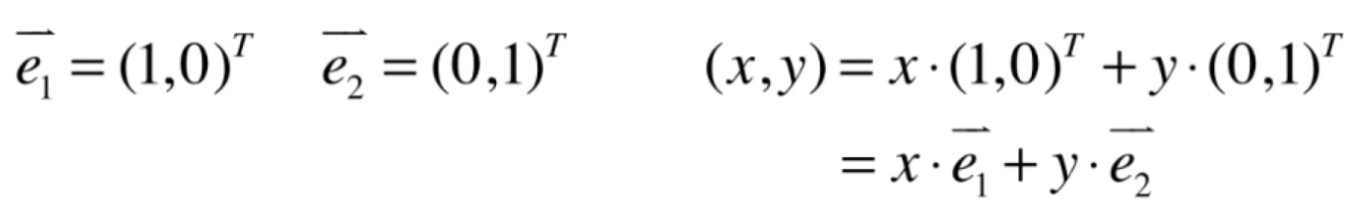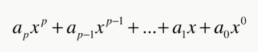害怕并不代表没有勇气,真正的行动才是最重要的。一个人究竟是英雄还是懦夫,由行动决定。 -《创业维艰》
此手记基于慕课网liuyubobobo老师的线代课程,感谢老师
线性系统
- 线性系统:未知数只能是一次方项
- 消元法
- 一个方程的左右两边同时乘以一个常数
- 一个方程加(减)另一个方程
- 交换两个方程的位置
- 使用矩阵来消元(高斯消元):
- 构建增广矩阵。其实,未知数的表示并没有意义,反而我们通过列数来表示未知数的个数,而行数代表线性系统有几个方程
- 第n行的第n个元素叫做主元(pivot),将主元化为1
- 当主元没有值时,我们可以交换行的位置来去掉这个约束。(通常是和当前主元位置最大的行来交换,这样可以尽量小的避免误差)
- 当求出一个未知值时,我们通过回代或者时高斯约旦消元法来求的剩下的值
- Gauss-Jordan Elimination
- 前向过程(从上到下)
- 1.选择最上的主元,化为1
- 2.主元下面的所有行减去主元所在行的某个倍数,使得主元下面所有元素都为0
- 后向过程(从下到上)
- 1.选择最下的主元
- 2.主元上面的所有行减去主元所在行的某个倍数,使得主元上面所有元素都为0
- 本质:寻找一系列初等矩阵E,使得:Ep·…·E3·E2·E1·A=rref(A)
- 前向过程(从上到下)
结构
- 行最简形式 reduced row echelon form(RREF)
- 阶梯型矩阵
- 全零行必须在最下面
- 非零行的第一个元素(主元)为1
- 主元所在列的其他元素均为0
- 阶梯型矩阵
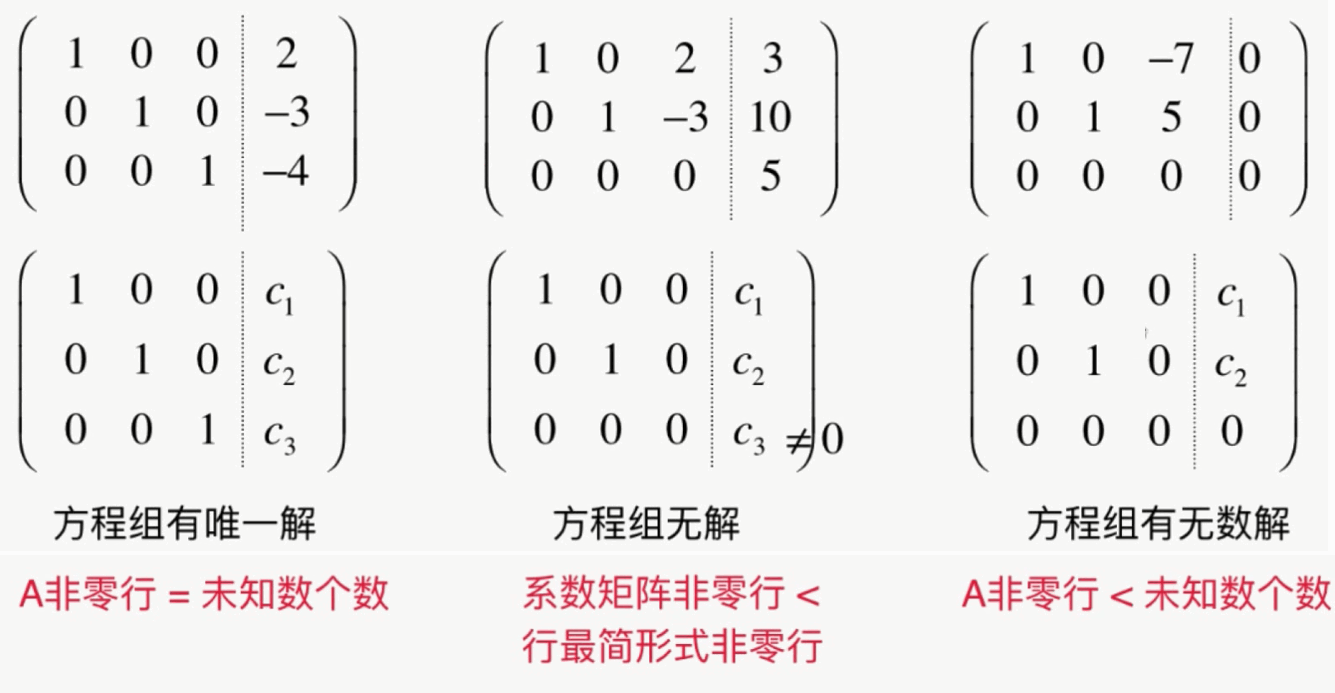
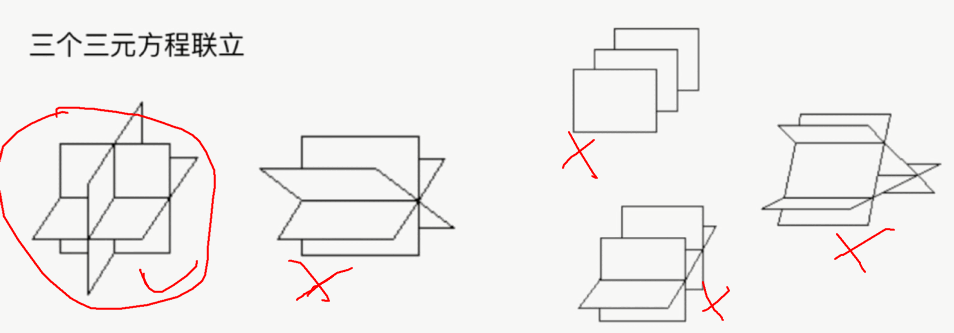
- n个未知数有n个方程,才可能有唯一解
- 方程组个数小于未知数个数,一定没有唯一解
当然,对于行最简形式,系数矩阵的非零行不可能大于未知数个数,这样的话,就可以去除无解的情况
又因为行最简形式,系数矩阵的非零行等于未知数个数:一定有唯一解
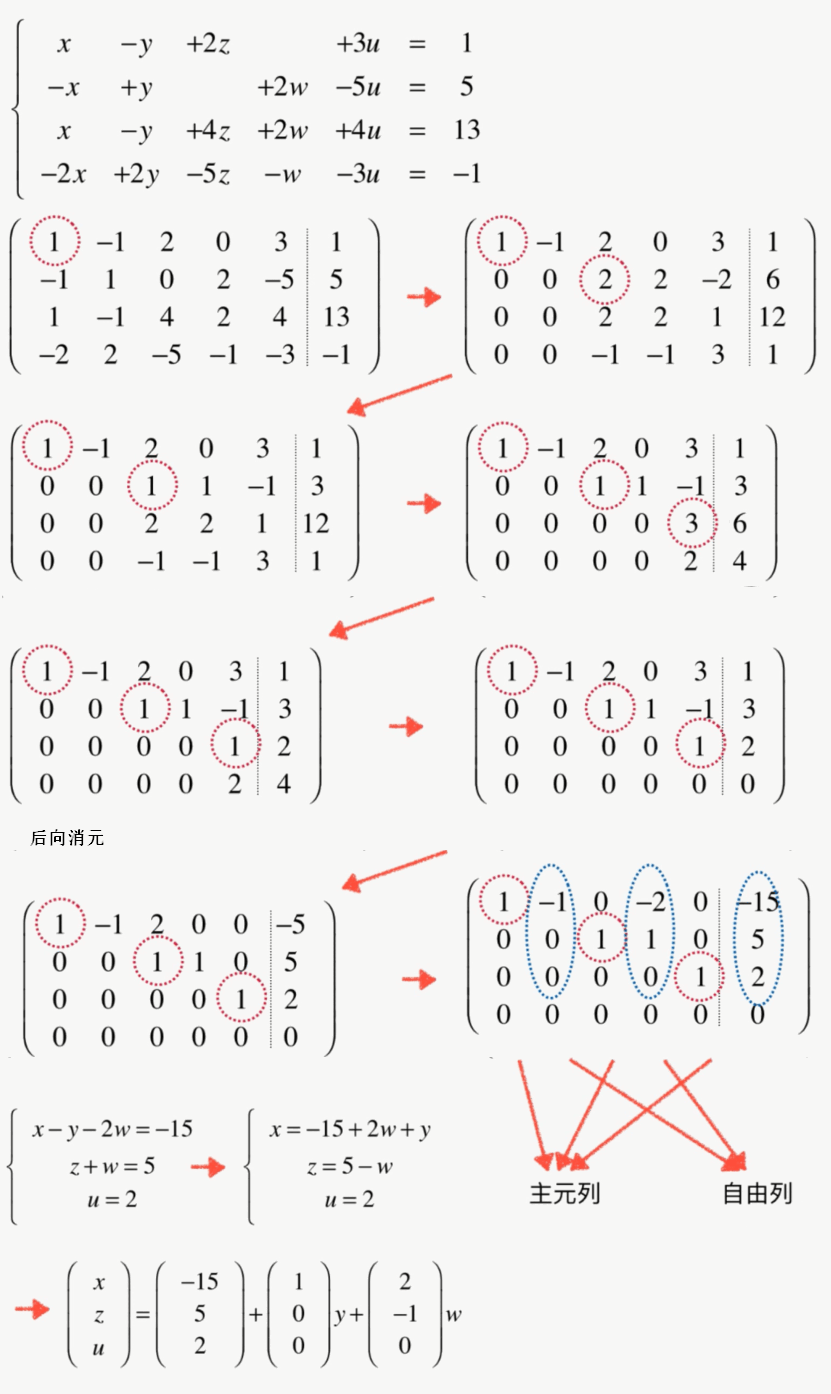
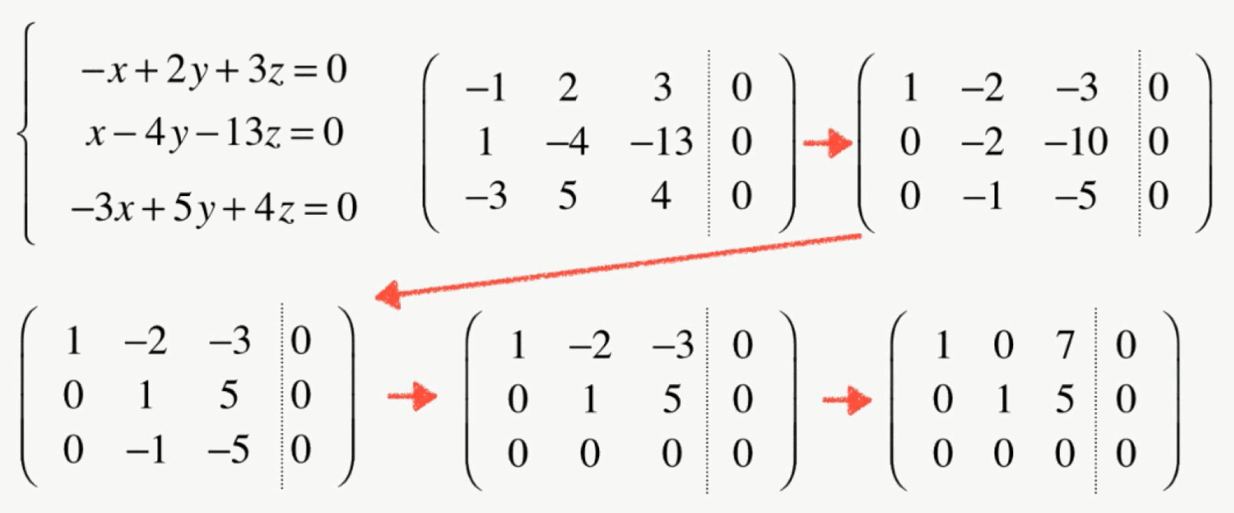
更一般的高斯约旦消元-案例
齐次线性方程组
- 肯定有解
- 最后一列肯定永远为零
- 最后一列肯定永远为零,解的过程可以只对系数矩阵做操作
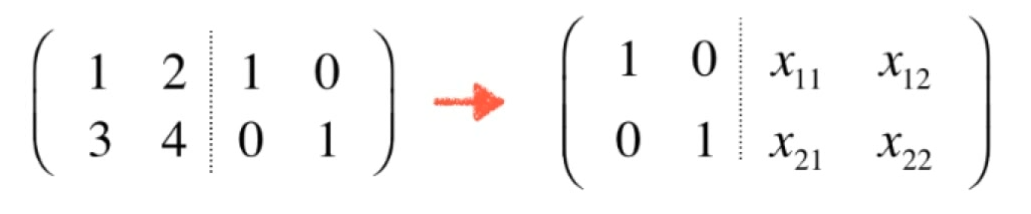
求矩阵的逆
- 对于一个方阵来说,它的逆不可能有无数解。要么有,要么没有
- 系数矩阵化为行最简形式时有0行时无解
- 如果一个方阵A有右逆B,则B也是A的左逆,即B是A的逆
初等矩阵
- 初等矩阵是指由单位矩阵经过一次三种矩阵初等变换得到的矩阵。通常记做E
矩阵的某一行乘以一个常数
矩阵的一行加(减)另一行
交换矩阵的两行
-
初等矩阵对单位矩阵进行一次初等变换得到,因为初等变换是可逆的,所以初等矩阵是可逆的
-
使用求解A的逆该方法和直接使用高斯消元法来求解的过程的时间复杂度大体上是一致的。
-
但是如果在A不变,b会变化的条件下,大大加快计算速度
-
对于方阵A(以下命题全部等价)
-
矩阵A可逆(A是非奇异矩阵) -> 矩阵A不可逆(A是奇异矩阵) ,存在零行
-
线性系统Ax=0只有唯一解,x=0
-
rref(A)=I
-
A可以表示成一系列初等矩阵的乘积
-
Ax=b只有唯一解
矩阵的LU分解
提高计算效率为目的。
在解Ax=b的过程中,LU分解:O(0.5n3)
L·U·x=b
设Ux=y,L·y=b,O(n2)求出y,U·x=y,O(n2)求出x
在解Ax=b的过程中,LU分解:O(0.5n3)+2O(n2),求逆:O(2n3)+ O(n^2)
LU分解可以用于非方阵
-
将矩阵A分解为A=L·U
-
L:Lower Triangle Matrix 下三角矩阵
-
-
U:Upper Triangle Matrix 上三角矩阵
-
-
矩阵可以进行LU分解的条件:
- 对A进行高斯消元的过程,不需要交换两行的位置,不过可以通过PLU分解实现
PLU
另一种情况
- 继续高斯消元,需要交换矩阵的两列
- 初等变换只能交换矩阵的两行
- 交换矩阵的两列,需要右乘以置换矩阵
线性组合
向量的两个最基本的运算构建了线性代数中最重要的一个概念:线性组合
- 三维空间中的任何一个向量都是其三个标准单位向量的一个线性组合
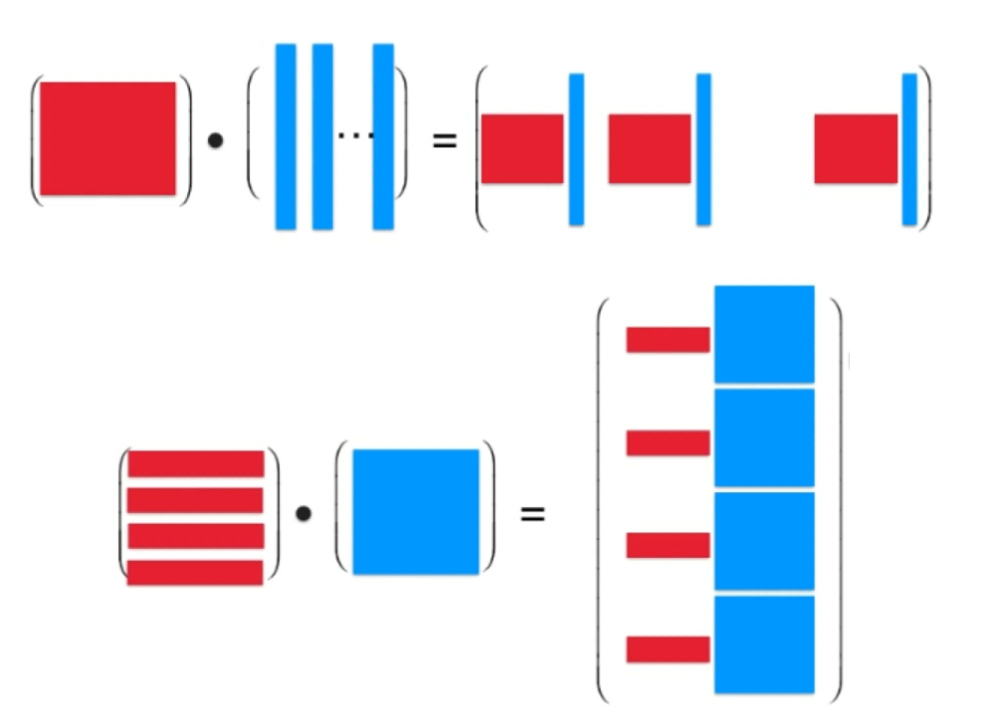
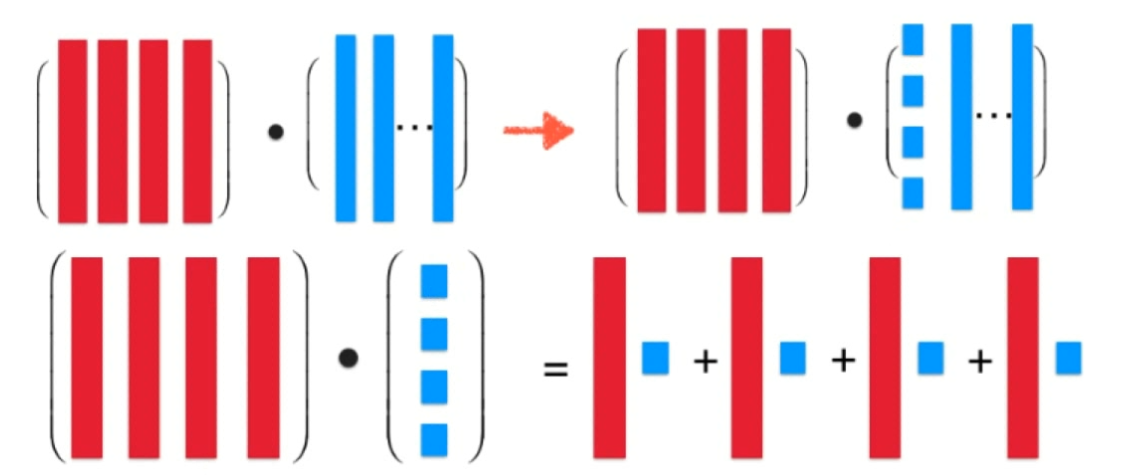
- 矩阵和向量的乘法,可以看做是矩阵的列向量的一个线性组合
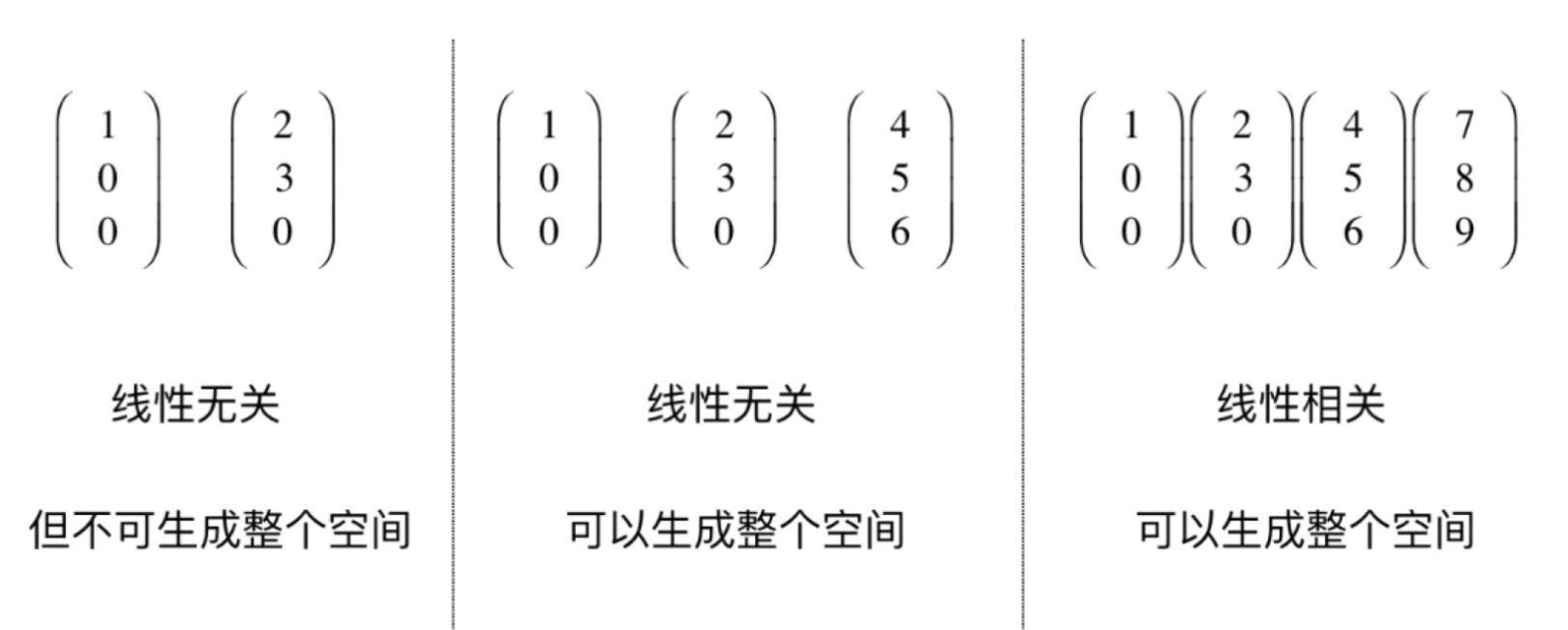
线性相关
- 任何一个向量都不可以表示成其他向量的线性组合。
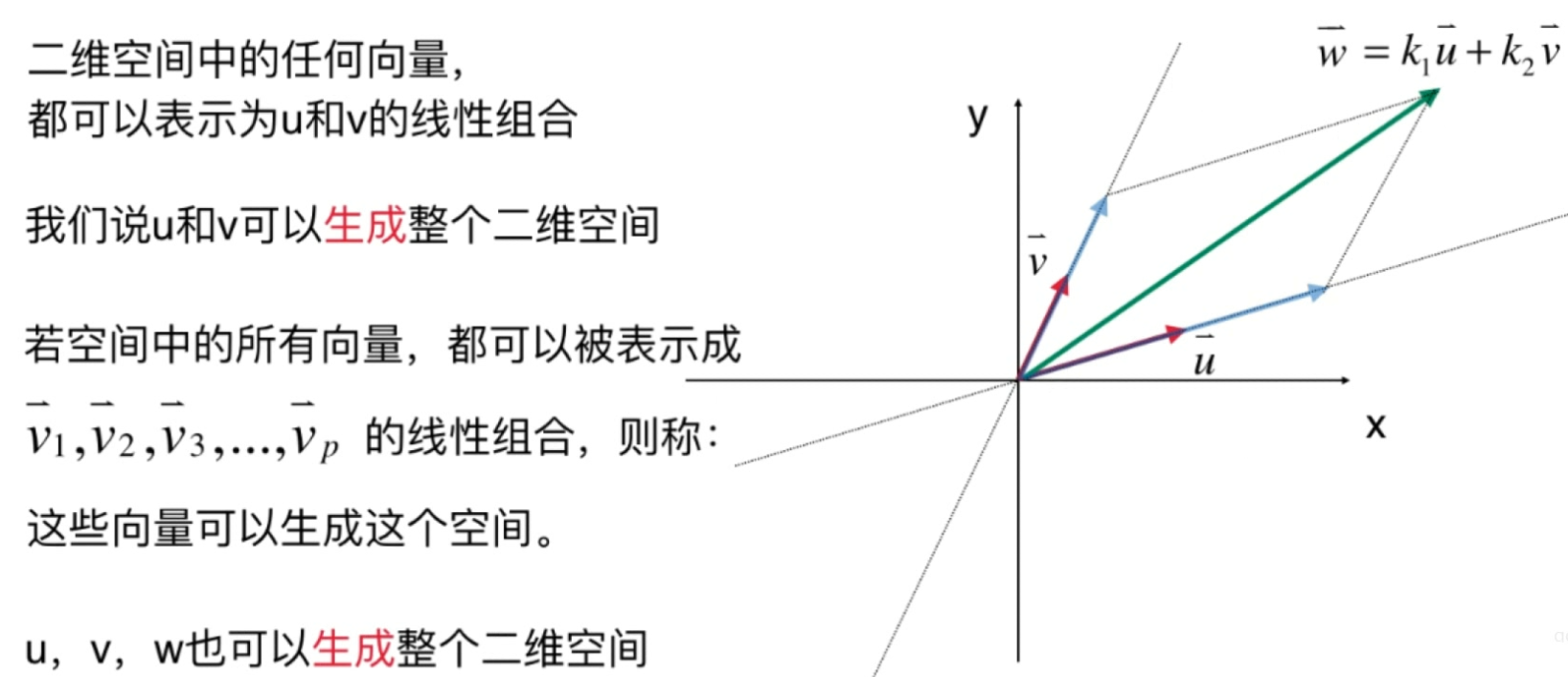
生成空间
- 若m个向量生成n维空间,m最小为n
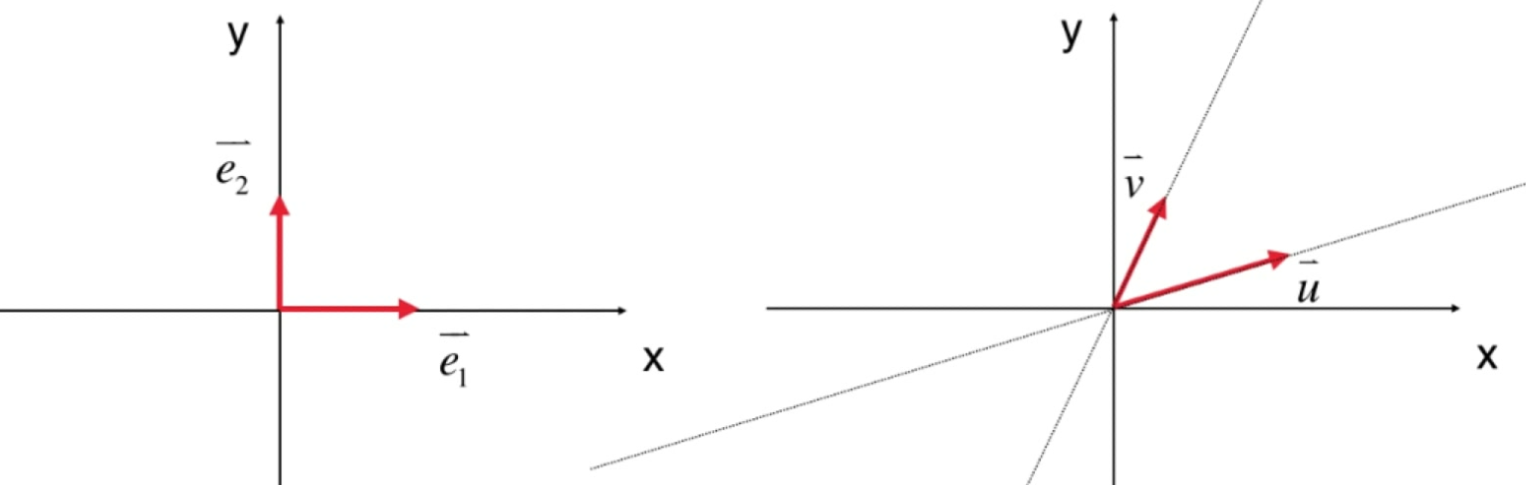
- e1,e2也是二维空间的基;u,v也是二维空间的基。他们应该具有同样的性质!
- 在二维空间,任何一个向量(或者是点)都可以表示成e1,e2的线性组合。
- 在二维空间,任何一个向量(或者是点)都可以表示成u和v的线性组合!且表示方法唯一。
- 推广:在n维空间,如果给定一组基。
- 推广:任何一个向量(或者是点)都可以表示成这组基的线性组合!
空间
- 空间是一个集合
- 欧几里得空间是有序实数元组的集合
- (6,66)属于二维欧几里得空间; R^2
- (3.14,0,sqrt(2))属于三维欧几里得空间;R^3
- 欧几里得空间是点集;是起点为原点的向量集合,属于向量空间
- 向量空间:一个集合,集合中的元素可以定义两种运算:加法和数量乘法,使得满足十条性质。
- 对于一个向量空间V
- 如果u,v都属于V,则u+v属于V
- 如果u属于V,k是一个实数,则ku属于V
- 在数学上,被称为封闭(closure)
- 向量空间十条定理
- 加法交换律:u+v=v+u
- 加法结合律:(u+v)+w=u+(v+w)
- 存在O属于向量空间,使得u+O=u
- 对于每一个u存在-u,使得u+(-u)=O
- 如果u属于V,k是一个实数,则ku 属于V
- 数量乘结合律:(kc)u=k(cu)
- 数量乘分配律:k(u+V)=ku+kv
- 数量乘分配律:(k+c)u=ku+cu
- 1*u = u
- 对于一个向量空间V
广义向量空间
- 为了区别,通常把非欧几里得空间的向量空间,称为广义向量空间。
- 所有的多项式,构成一个向量空间。
- 加法:多项式加法;数量乘法:多项式乘以一个数
- 加法:多项式加法;数量乘法:多项式乘以一个数
- 所有的n阶方阵,构成一个向量空间。
- 所有的m*n的矩阵,构成一个向量空间。
- 加法:矩阵加法;数量乘法:矩阵数量乘法。
- 加法:矩阵加法;数量乘法:矩阵数量乘法。
点击查看更多内容
1人点赞
评论
共同学习,写下你的评论
评论加载中...
作者其他优质文章
正在加载中
感谢您的支持,我会继续努力的~
扫码打赏,你说多少就多少
赞赏金额会直接到老师账户
支付方式
打开微信扫一扫,即可进行扫码打赏哦