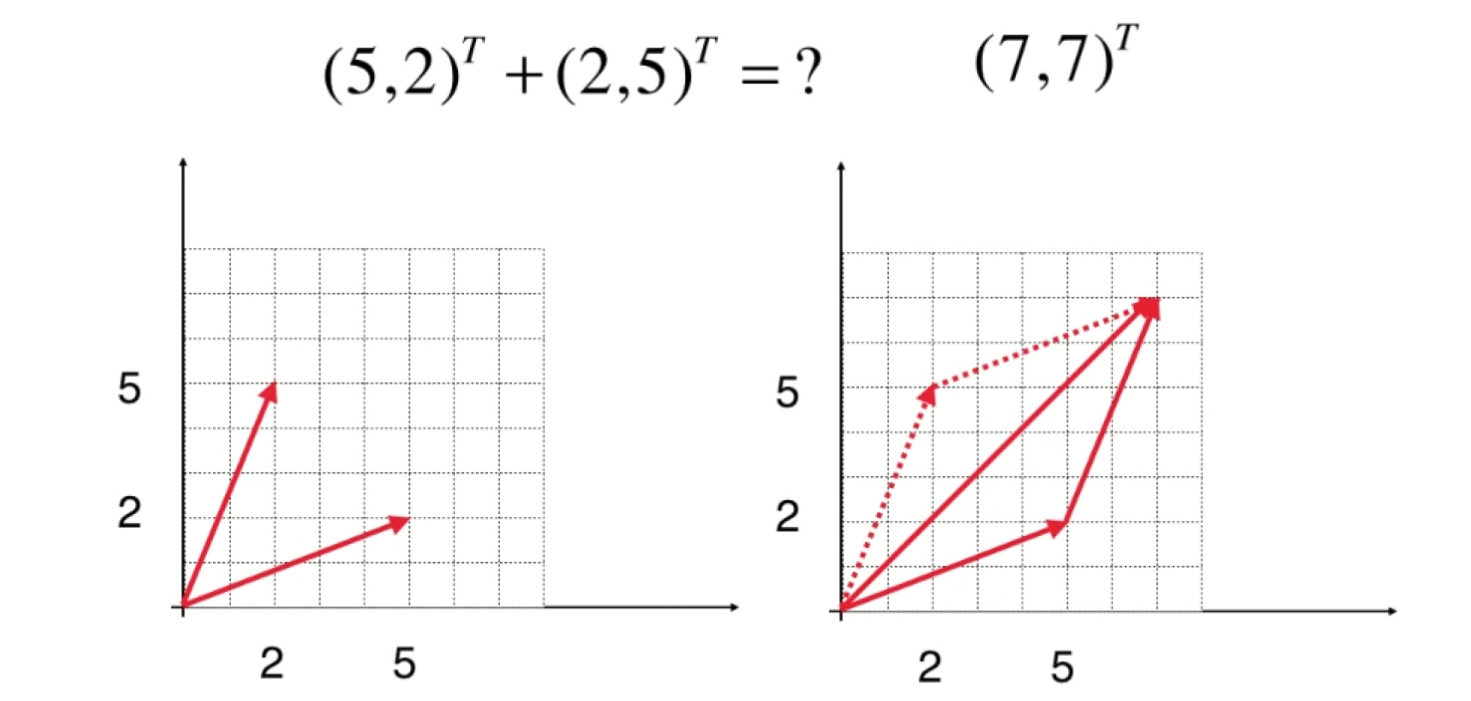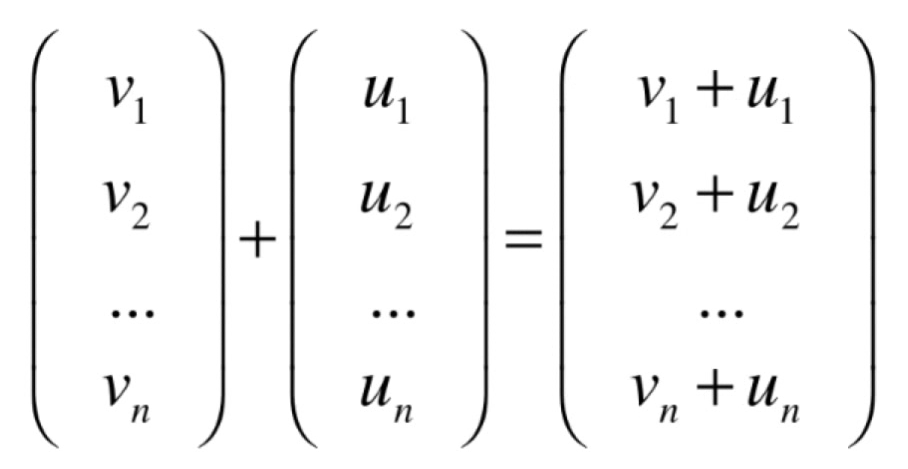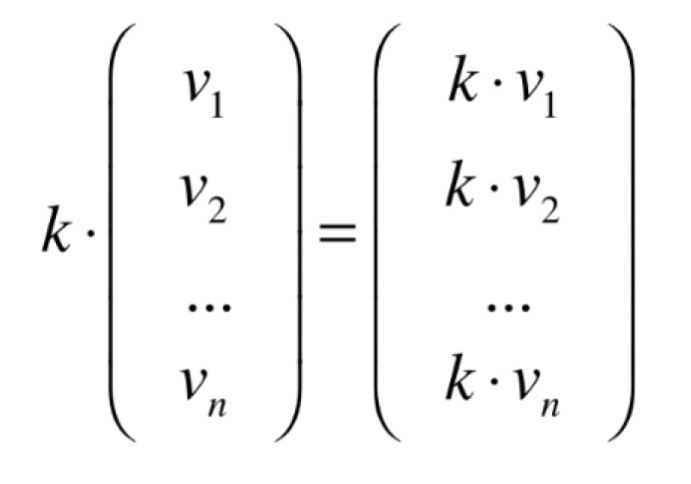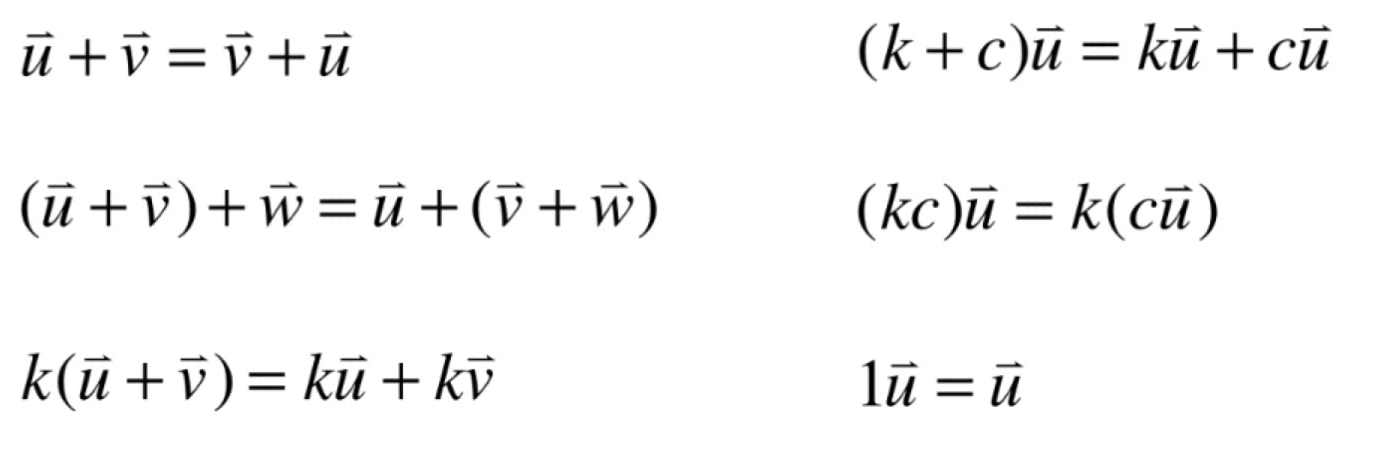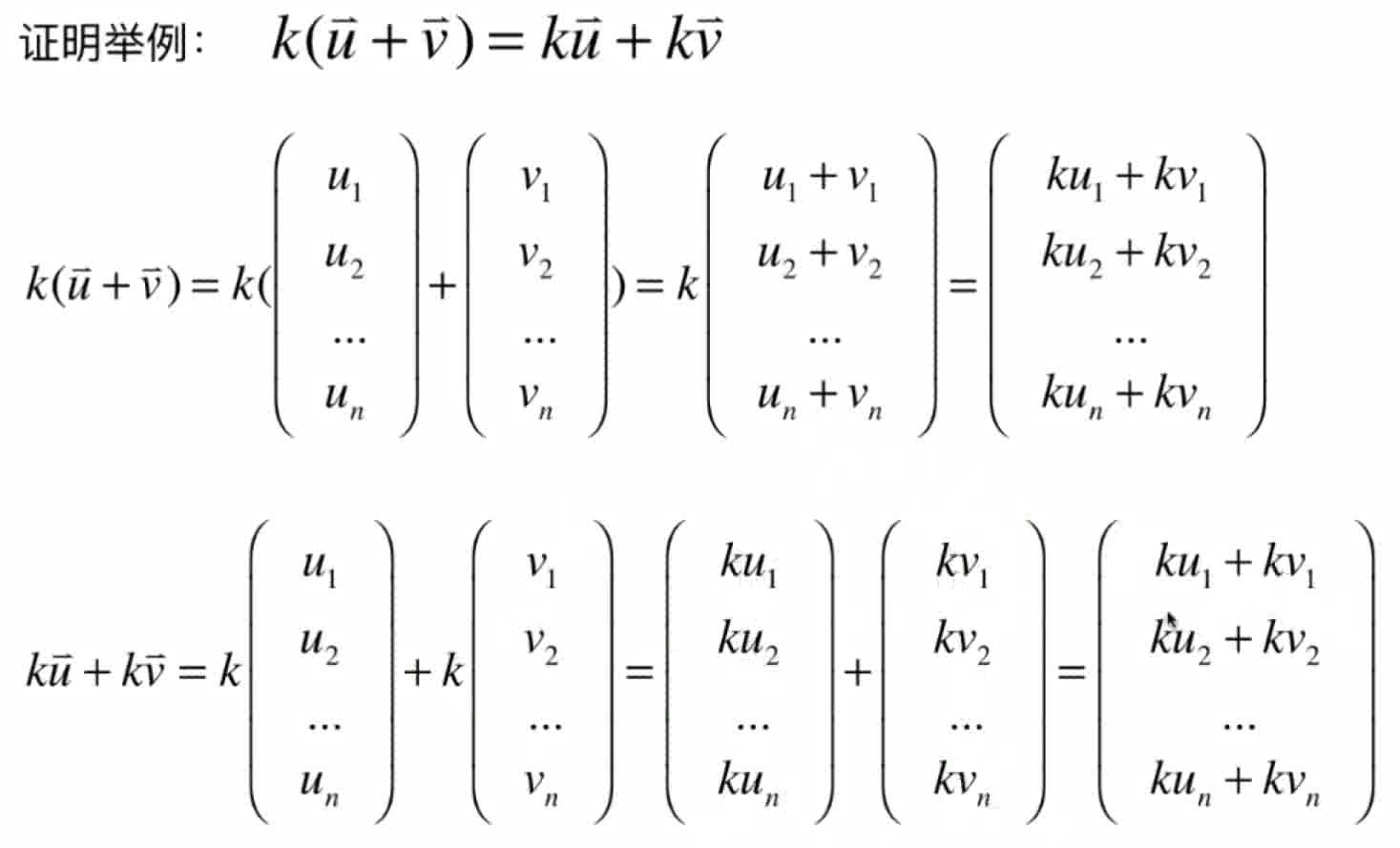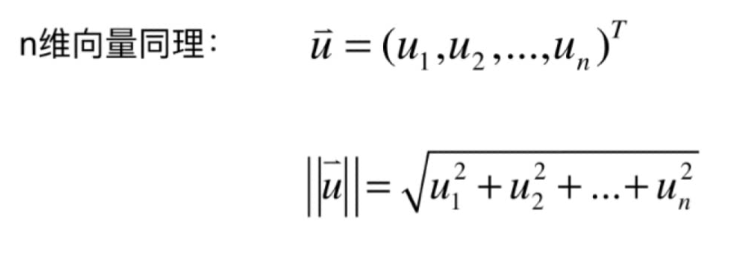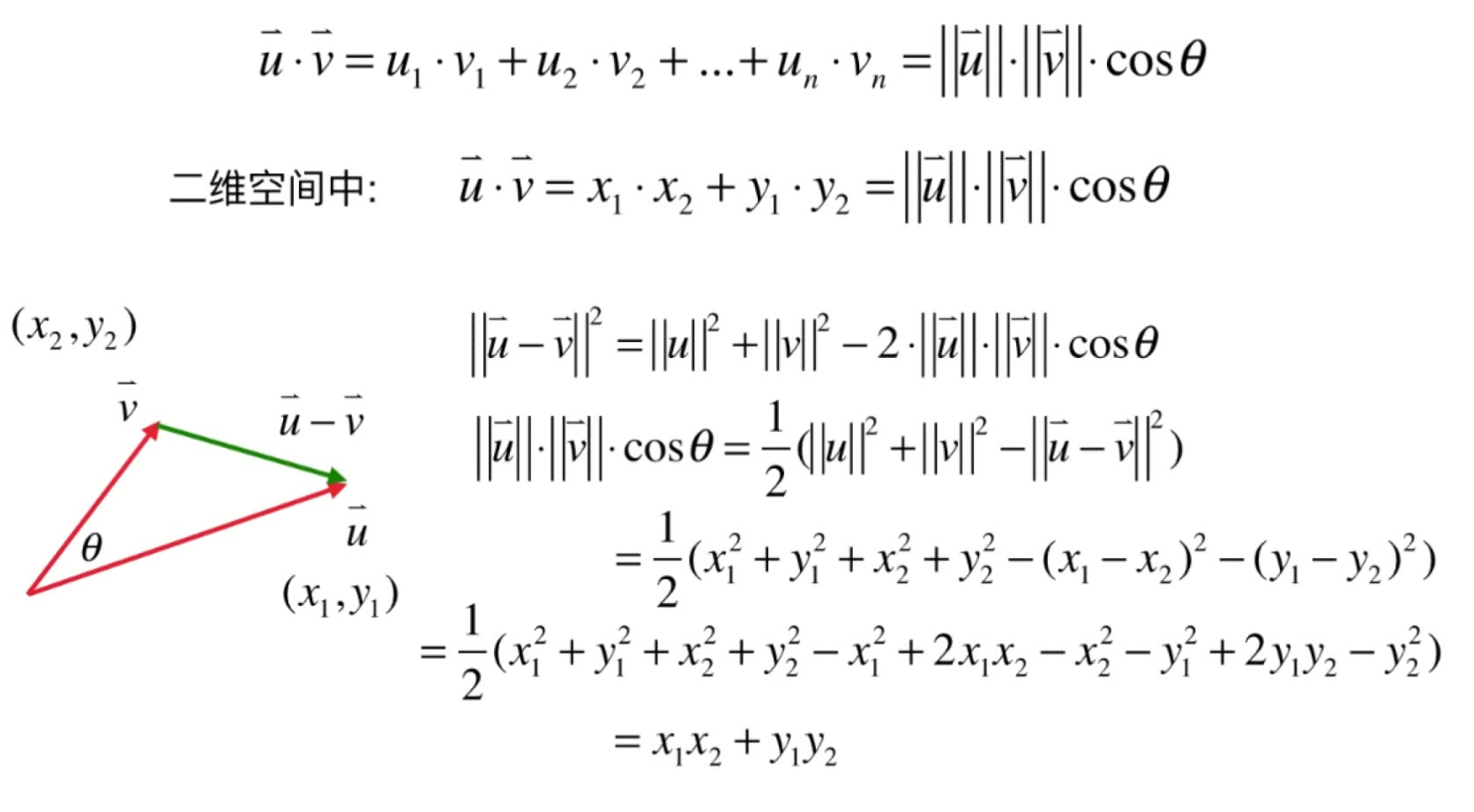非科班程序员才不知道的向量

程序的功能单位不宜过大，太大的函数容易掩盖错误，就像一个大城市隐藏着逃犯一样。这样的软件很难阅读，很难测试，也很难调试。（《自下而上的编程》，by Paul Graham）

向量

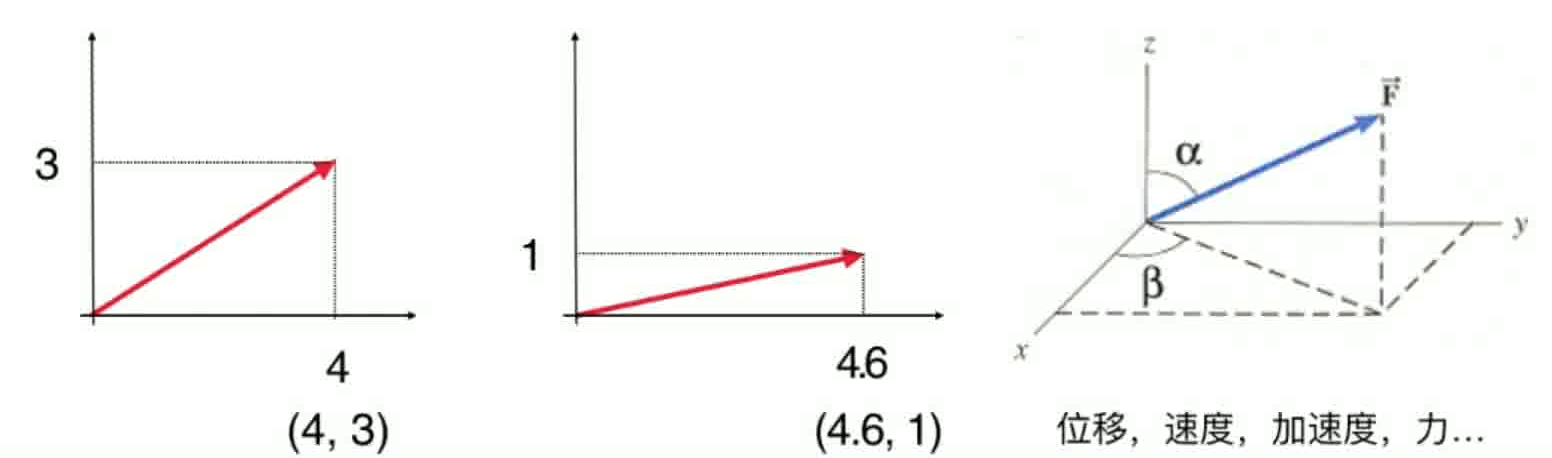
• 为什么线性代数这么重要？从研究一个数拓展到研究一组数
• 一组数的基本表示方法——向量（Vector)
• 向量（Vector)是线性代数研究的基本元素（一组有序的数）
  • 一个数：666 一组数：（6，66，666）
  • 最基本的出发点：表示方向
    
• 两个视角看似不同，但可以互相转换
  • 一个方向，就是一个点（有向线段 ≈ 空间中的点）
• 空间中的一个点，可以看做从原点指向这个点的一个方向
• 在学习初始，使用方向的视角，更直观，更形象
• 定义
• 和向量相对应，一个数字，称为标量
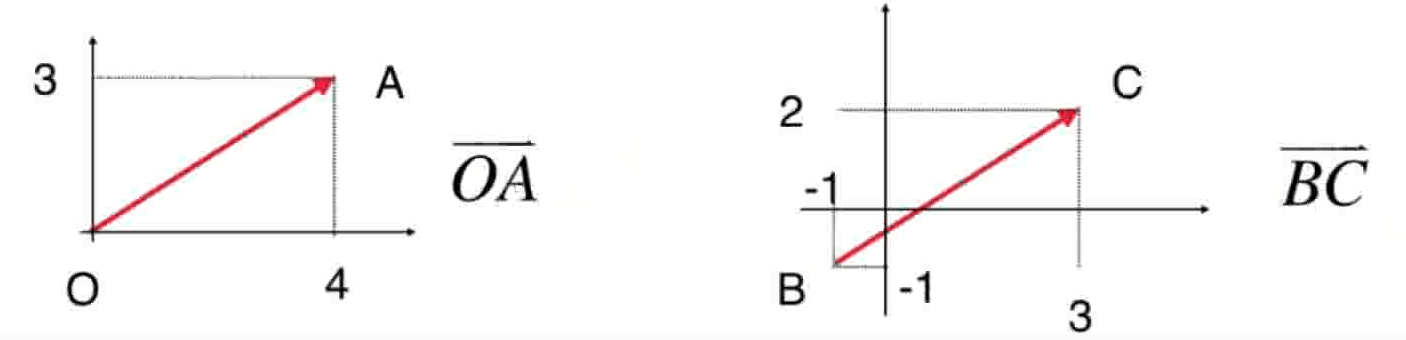
• 代数，用符号代表数。和标量相区别，向量的符号画箭头
• 个别情况下，尤其是几何学中，我们会考虑向量的起始点
  

向量相加

• 先向x移动5个单位
• 再向y移动2个单位
• 再向x移动2个单位
• 再向y移动5个单位
• 先向x移动5个单位
• 再向y移动2个单位
• 再向x移动2个单位
• 再向y移动5个单位
• 总共向x移动7个单位
• 总共向y移动7个单位
  
  

数量相乘

• k×(a,b)^T= (ka,kb)^T
• 向x移动k次a个单位
• 再向y移动k次b个单位
• 总共向x移动ka个单位
• 总共向y移动kb个单位
  

基本性质

零向量

• 零向量O没有箭头
  
  

长度（向量的模）

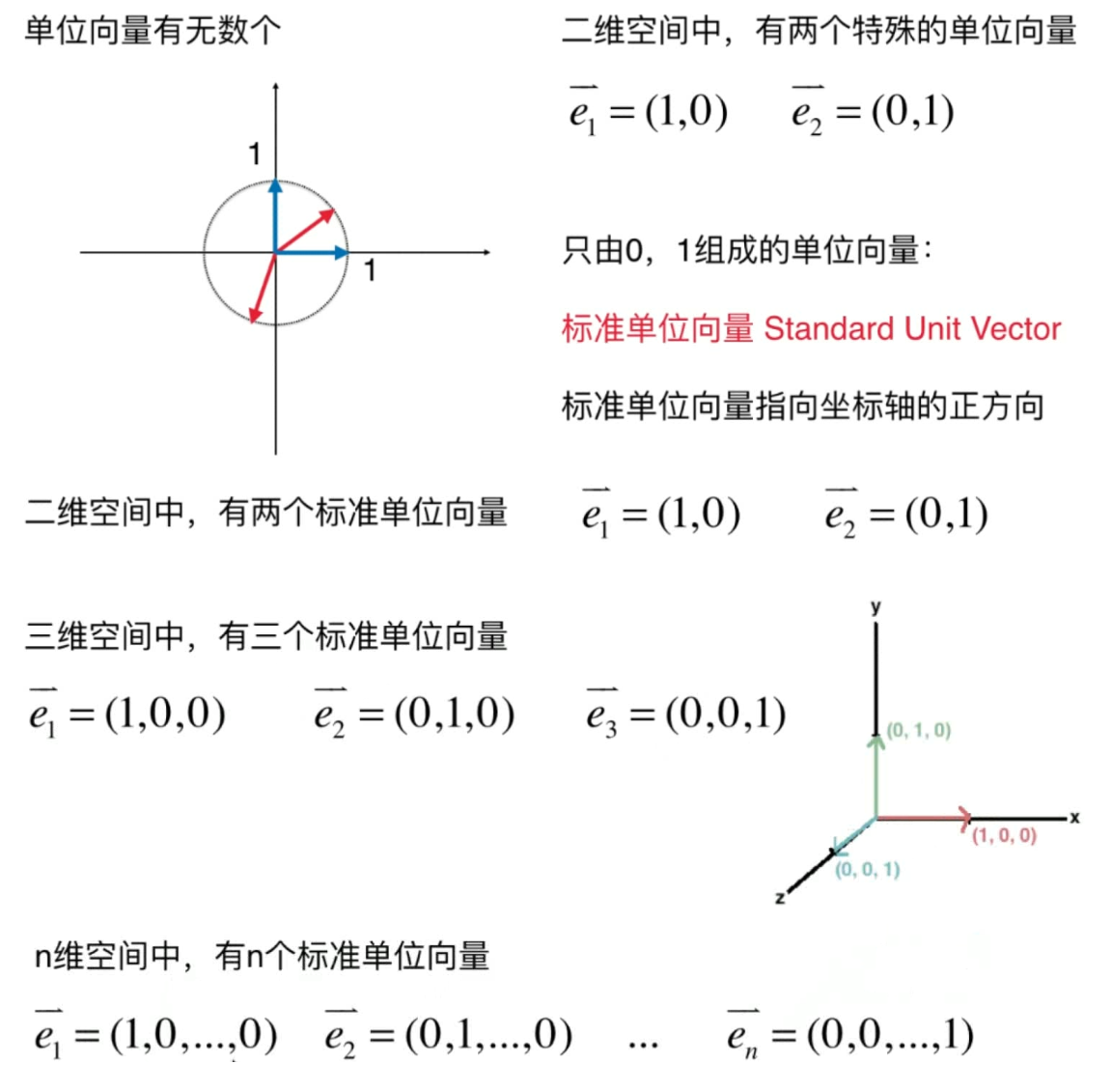
单位向量 unit vector

点乘

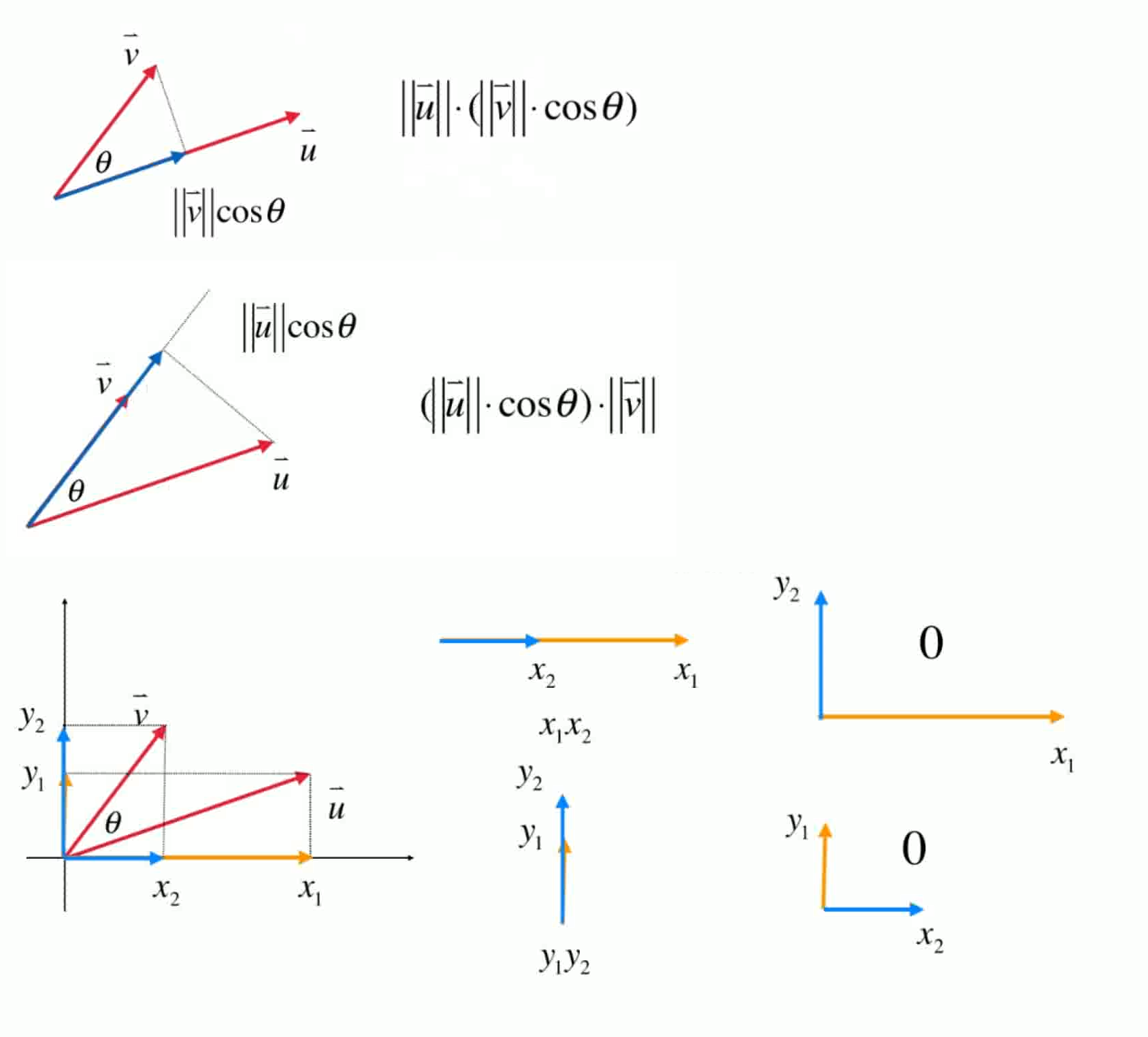
直观化理解

• x1和y2没有关系，结果为零；x2和y1没有关系，结果为零