C++实现二叉排序树

1.定义

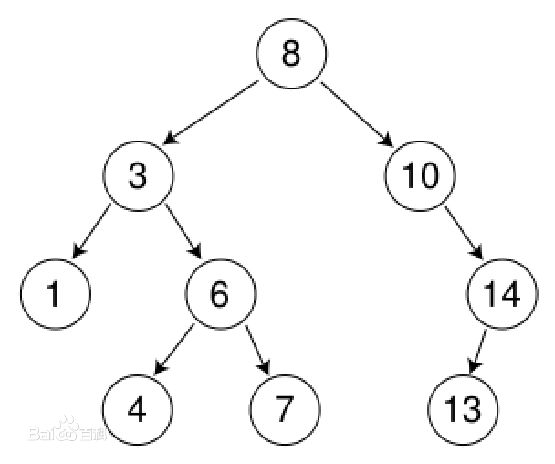
二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），亦称二叉搜索树。

二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：

（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；

（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；

（3）左、右子树也分别为二叉排序树；

（4）没有键值相等的节点。

简言之，左子树小于父节点，右子树大于父节点的二叉树就是二叉排序树

回到顶部

2.代码实现

2.1 插入元素：

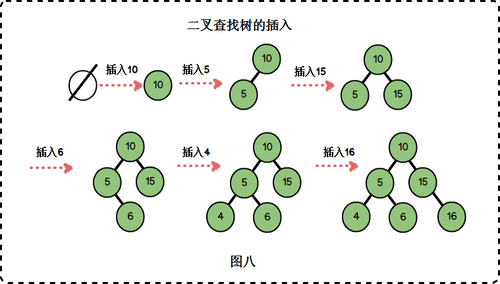
假设我们要为数组 a[] = {10 ， 5 ， 15 ， 6 ， 4 ， 16 }构建一个二叉排序树，我们按顺序逐个插入元素。

插入过程是这样的：

• 如果是空树，则创建一个新节点，新节点作为根，因此以元素10构建的节点为该二叉查找树的根。

• 插入5，5比10小，与10的左孩子节点进行比较，10的左孩子节点为空，进行插入。

• 插入15，15比10大，与10的右孩子节点进行比较，10的右孩子节点为空，进行插入。

• 插入6，6比10小，与10的左孩子节点5比较；6比5大，与5的右孩子节点进行比较，5的右孩子为空，进行插入。

• 插入4，4比10小，与10的左孩子节点5比较；4比5小，与5的左孩子节点进行比较，5的左孩子为空，进行插入。

• 插入16，16比10大，与10的右孩子节点15比较；16比15大，与15的右孩子节点进行比较，15的右孩子为空，进行插入。

从这个过程我们可以总结出插入新元素的步骤：

• 寻找元素合适的插入位置：新元素与当前结点进行比较，若值大于当前结点，则从右子树进行寻找；否则从左子树进行寻找.

• 找到插入位置之后，以元素的值构建新节点，插入二叉排序树中

/*插入函数*/template <typename T>void BSTree<T>::insert(T key)
{
    BSNode<T>* pparent = nullptr;
    BSNode<T>* pnode = root;    while (pnode != nullptr)        //寻找合适的插入位置    {
        pparent = pnode;        if (key > pnode->value)
            pnode = pnode->rchild;        else if (key < pnode->value)
            pnode = pnode->lchild;        else            break;
    }

    pnode = new BSNode<T>(key);    if (pparent == nullptr)            //如果是空树    {
        root = pnode;                //则新节点为根    }    else
    {        if (key > pparent->value)
        {
            pparent->rchild = pnode;//新节点为其父节点的右孩子        }        else
            pparent->lchild = pnode;//新节点为其父节点左孩子    }
    pnode->parent = pparent;        //指明新节点的父节点};

2.2 删除元素：

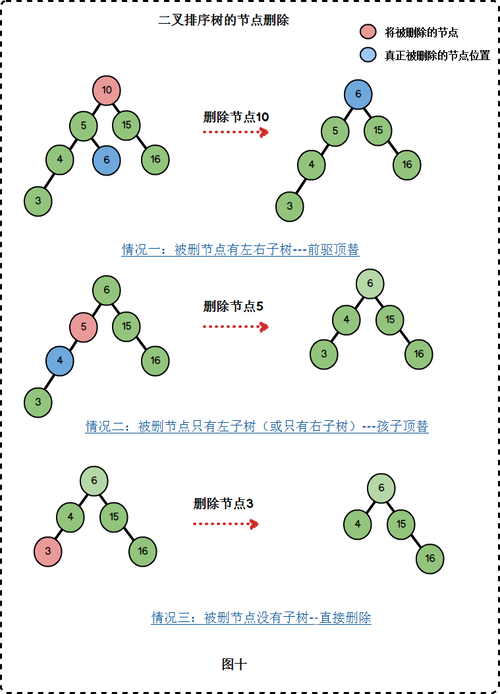
删除二叉排序树的某个节点有三种情况：

• 被删除节点同时有左子树与右子树。

• 被删除节点只有左子树或只有右子树。

• 被删除节点没有子树。

对于第一种情况，我们的处理方式是将前驱节点的值保存在当前结点，继而删除前驱节点。
对于第二种情况，我们直接用子树替换被删节点。
对于第三种情况，我们可以直接删除节点。

template <typename T>void BSTree<T>::remove(BSNode<T>* pnode, T key)
{    if (pnode != nullptr)
    {        if (pnode->value == key)
        {
            BSNode<T>* pdel = nullptr;            if (pnode->lchild == nullptr || pnode->rchild == nullptr)
                pdel = pnode;                    //情况二、三：被删节点只有左子树或右子树，或没有孩子            else
                pdel = predecessor(pnode);      //情况一：被删节点同时有左右子树，则删除该节点的前驱                                                //此时，被删节点只有一个孩子（或没有孩子）.保存该孩子指针
            BSNode<T>* pchild = nullptr;            if (pdel->lchild != nullptr)
                pchild = pdel->lchild;            else
                pchild = pdel->rchild;            //让孩子指向被删除节点的父节点            if (pchild != nullptr)
                pchild->parent = pdel->parent;            //如果要删除的节点是头节点，注意更改root的值            if (pdel->parent == nullptr)
                root = pchild;            //如果要删除的节点不是头节点，要注意更改它的双亲节点指向新的孩子节点            else if (pdel->parent->lchild == pdel)
            {
                pdel->parent->lchild = pchild;
            }            else
            {
                pdel->parent->rchild = pchild;
            }            if (pnode->value != pdel->value)
                pnode->value = pdel->value;
            delete pdel;
        }        //进行递归删除        else if (key > pnode->value)
        {
            remove(pnode->rchild, key);
        }        else remove(pnode->lchild, key);
    }
};

2.3 查找指定元素的节点（While循环)：

判断当前结点是否为空指针，不是空指针进入

key直接和当前结点value相等，return当前结点

key大于当前结点value，将右子节点赋予当前结点

key小于当前结点value，将左子节点赋予当前结点

直到key等于当前结点或者当前结点为空停止while循环

/*查找指定元素的节点（非递归）*/template <typename T>BSNode<T>* BSTree<T>::search_Iterator(T key)
{
    BSNode<T> * pnode = root;    while (pnode != nullptr)
    {        if (key == pnode->value)    //找到            return pnode;        if (key > pnode->value)        //关键字比节点值大，在节点右子树查找
            pnode = pnode->rchild;        else
            pnode = pnode->lchild; //关键字比节点值小，在节点左子树查找    }    return nullptr;
};

2.4 查找指定元素的节点（递归)：

逻辑同上，将pnode替换为左或者右子节点，递归调用之

/*查找指定元素的节点（递归）*/template <typename T>BSNode<T>* BSTree<T>::search_recursion(T key)
{    return search(root, key);
};/*private:search()*//*递归查找的类内部实现*/template <typename T>BSNode<T>* BSTree<T>::search(BSNode<T>* & pnode, T key)
{    if (pnode == nullptr)        return nullptr;    if (pnode->value == key)        return pnode;    //cout << "-->" << pnode->value << endl; //可以输出查找路径    if (key > pnode->value)        return search(pnode->rchild, key);    return search(pnode->lchild, key);
};

2.5 寻找其前驱节点：

前驱和后继结点说明：

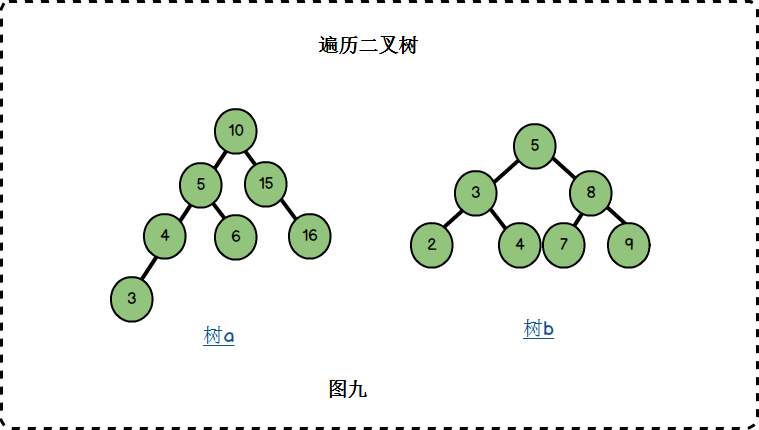
对于一棵二叉排序树，中序遍历时刚好可以输出一个非递减的序列。例如中序遍历图九树a：3 4 5 6 10 15 16，则可称：

• 4是5 前驱节点，6是5的后继节点

• 6是10的前驱节点，15是10的后继节点

前驱结点：

1. 它有左子树，则左子树的最右结点为其前驱节点

2. 它没有左子树，且它本身为右子树，则其父节点为其前驱节点

3. 它没有左子树，且它本身为左子树，则它的前驱节点为“第一个拥有右子树的父节点”

判断当前结点左子树是否为空，不为空进入

左孩子赋予当前结点，与情况1对应

判断父节点是否是空指针并且当前结点本身是否是左子树

本身是左子树，进入循环，是第三种情况。不是左子树，是第二种情况

/*寻找其前驱节点*//*一个节点的前驱节点有3种情况：
1. 它有左子树，则左子树最右结点为其前驱节点
2. 它没有左子树，且它本身为右子树，则其父节点为其前驱节点
3. 它没有左子树，且它本身为左子树，则它的前驱节点为“第一个拥有右子树的父节点”*/template <typename T>BSNode<T>* BSTree<T>::predecessor(BSNode<T>* pnode)
{    if (pnode->lchild != nullptr)
    {
        pnode = pnode->lchild;        while (pnode->rchild != nullptr)
        {
            pnode = pnode->rchild;
        }        return pnode;
    }

    BSNode<T>* pparent = pnode->parent;    while (pparent != nullptr && pparent->lchild == pnode)//如果进入循环，则是第三种情况；否则为第二种情况    {
        pnode = pparent;
        pparent = pparent->parent;
    }    return pparent;
};

2.6 寻找后继结点

1. 它有右子树；则其后继节点为其右子树的最左节点

2. 它没有右子树，但它本身是一个左孩子，则后继节点为它的双亲

3. 它没有右子树，但它本身是一个右孩子，则其后继节点为“具有左孩子的最近父节点”

判断当前结点右子树是否是空指针，不为空则进入

右子树赋予当前结点，当左子树不为空，将左子树赋予当前结点，对应情况1

如果当前结点没有右子树

判断父节点是否是空指针并且当前结点本身是否是右子树

本身是右子树，进入循环，对应情况3

本身不是右子树，不进入循环，对应情况2

/*寻找其后继节点*//*一个点有后继节点的情况：
1. 它有右子树；则其后继节点为其右子树的最左节点
2. 它没有右子树，但它本身是一个左孩子，则后继节点为它的双亲
3. 它没有右子树，但它本身是一个右孩子，则其后继节点为“具有左孩子的最近父节点”*/template <typename T>BSNode<T>* BSTree<T>::successor(BSNode<T>* pnode)
{    if (pnode->rchild != nullptr)
    {
        pnode = pnode->rchild;        while (pnode->lchild != nullptr)
        {
            pnode = pnode->lchild;
        }        return pnode;
    }

    BSNode<T>* pparent = pnode->parent;    while (pparent != nullptr&& pparent->rchild == pnode)
    {
        pnode = pparent;
        pparent = pparent->parent;
    }    return pparent;
};

2.7 寻找最大和最小元素数

这个比较好理解，根据二叉排序树定义，寻找最大就是不停地递归寻找右子树，直到右子树为空结束

寻找最小就是不停地递归寻找左子树，直到左子树为空

/*寻找最小元素*/template <typename T>T BSTree<T>::search_minimun()
{    return search_minimun(root);
};
template <typename T>T BSTree<T>::search_minimun(BSNode<T>* p)
{    if (p->lchild != nullptr)        return search_minimun(p->lchild);    return p->value;
};/*寻找最大元素*/template <typename T>T BSTree<T>::search_maximum()
{    return search_maximum(root);
};
template <typename T>T BSTree<T>::search_maximum(BSNode<T>*p)
{    if (p->rchild != nullptr)        return search_maximum(p->rchild);    return p->value;
};

参考：https://www.cnblogs.com/QG-whz/p/5168620.html#_label3_2

代码：https://github.com/cjy513203427/C_Program_Base/tree/master/60.%E4%BA%8C%E5%8F%89%E6%8E%92%E5%BA%8F%E6%A0%91

作者：Rest探路者            
出处：https://www.cnblogs.com/Java-Starter/p/10150717.html  本文版权归作者和博客园共有，欢迎转载，但未经作者同意请保留此段声明，请在文章页面明显位置给出原文连接