【深度学习】反向传播算法——原理介绍与推导（最强版）

简言

前面一系列的手记都是围绕【机器学习】展开的，机器学习是深度学习的基石，两者有着密不可分的关系。从本章节开始，将是【深度学习】的专题博客。每一篇博客都是自己的一次思想风暴，如果你对于自己的理解有些混乱，那么不妨从我的理解角度试试。深度学习，最核心的内容就是神经网络，而对于入门而言，反向传播算法（Back Propagation Neural Networks，简称BP算法），又是绕不开的一大障碍。网络上甚多讲述BP算法的博客，但是很多都有各种各样的问nonglege 题，导致自己学习起来相当吃力，所以在行文之初，我的目标便是希望能给出一份最全面、最清晰、零错误的BP算法手记。

1.神经元模型

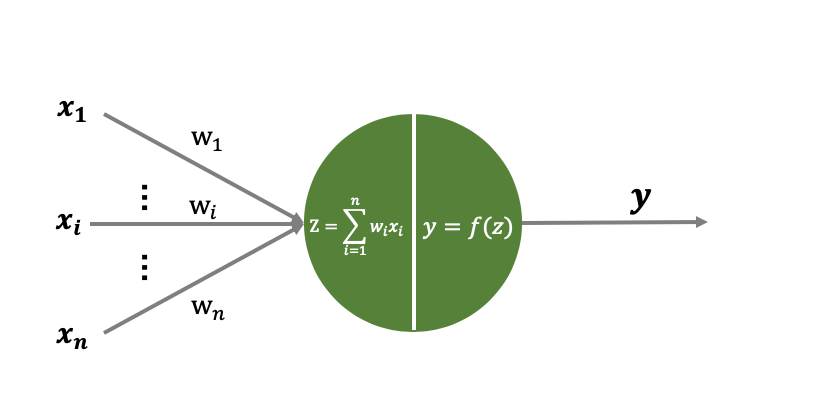
神经元是神经网络的基本组成单元，了解神经元的结构对了解整个神经网络大有裨益。目前神经网络采用的神经元模型为“M-P神经元模型”，该神经元模型与生物神经元模型类似，有输入端（树突）、输出端（轴突）、处理中枢（神经元中枢），模型如下所示：

注：上图所示的“M-P神经元”模型与实际的“M-P神经元”模型有所出处，具体细节可以参考西瓜书（神经网络章节）。此处如此介绍，是为了与下文叙述保持一致，且如此理解更为简单。

上图 $x1,x2,⋯,xnx_1,x_2,\cdots,x_n$ 表示神经元的多个输入， $w1,w2,⋯,wnw_1,w_2,\cdots,w_n$ 表示对应输入的权重参数（链接权重），神经元对输入的参数和其对应的权重进行线性组合得到 $z=∑i=1nwixiz=\sum_{i=1}^{n}w_ix_i$ ,随后将 $z$ 作为参数传递给激活函数 $y=f(⋅)y=f(\cdot)$ ,并最终得到神经元输出值 $y$ 。其中激活函数 $f(⋅)f(\cdot)$ 可以为多种激活函数，且激活函数均为非线性函数。

2.神经网络

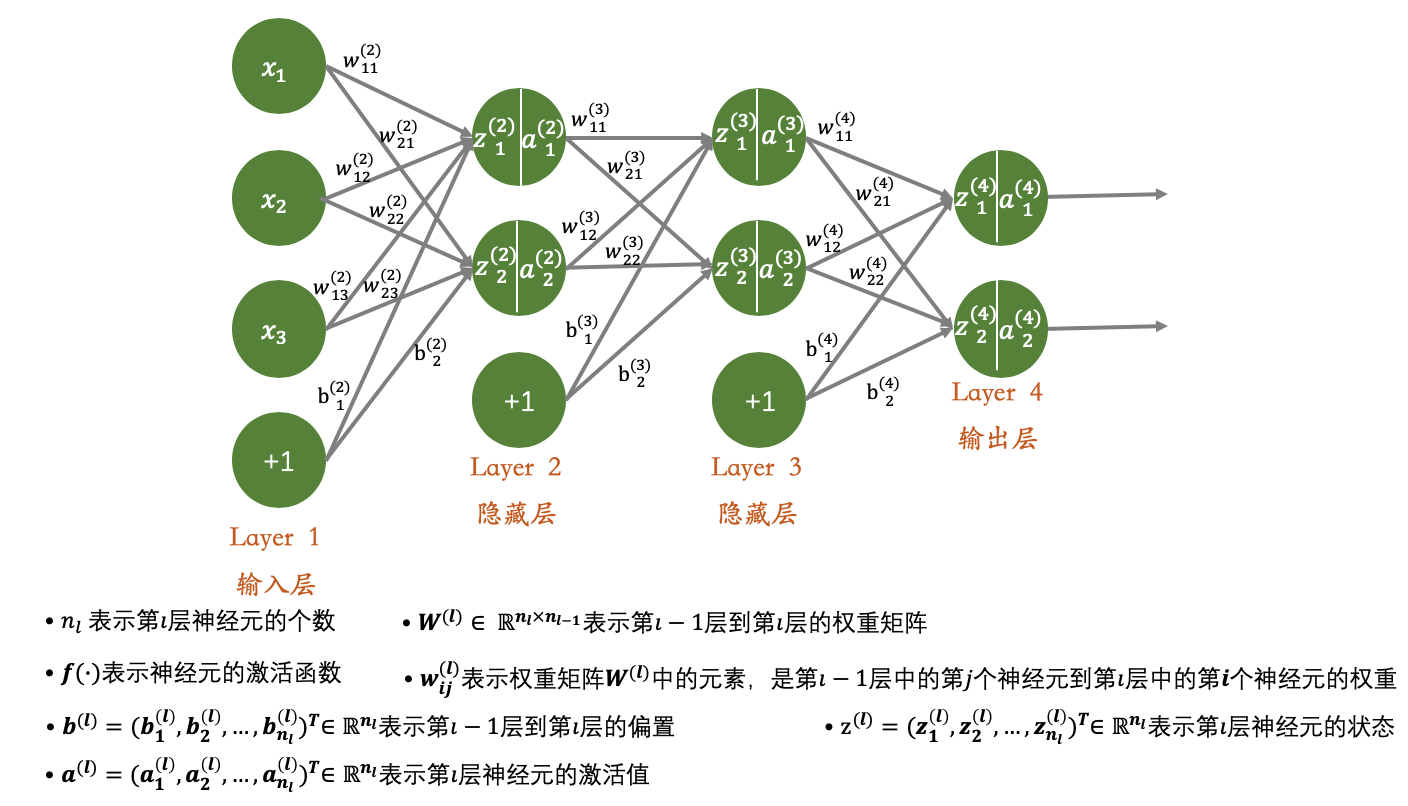
神经网络，是神经元按层结合的一个神经元网络。通常我们将输入（ $x_i$ ）与偏置( $b$ )也当做神经元处理（只是没有对应的处理函数），故我们经常见到的神经网络如下图所示：

其中的符号定义规则如图上的规则所示。其中" $+ 1$ "的神经元均为偏置项， $x_1,x_2,x_3$ 为输入项，对应于数据的三个属性。如上便为神经元的一般结构，当然，由于组合方式、神经元数量以及激活函数的多样化，导致神经网络的结构也多种多样，而此处的神经网络模型，仅限于本文。

对于神经网络模型的计算过程，主要分为两个部分：

前向传播算法
后向传播算法

前向传播算法，用于计算模型最终的输出结果；后向传播算法，用于减小模型输出结果与实际结果之前的误差，通过调整参数权重来优化模型。故，神经网络就是通过前向传播与后向传播算法的循环迭代，来训练模型，进而进行预测或者分类。

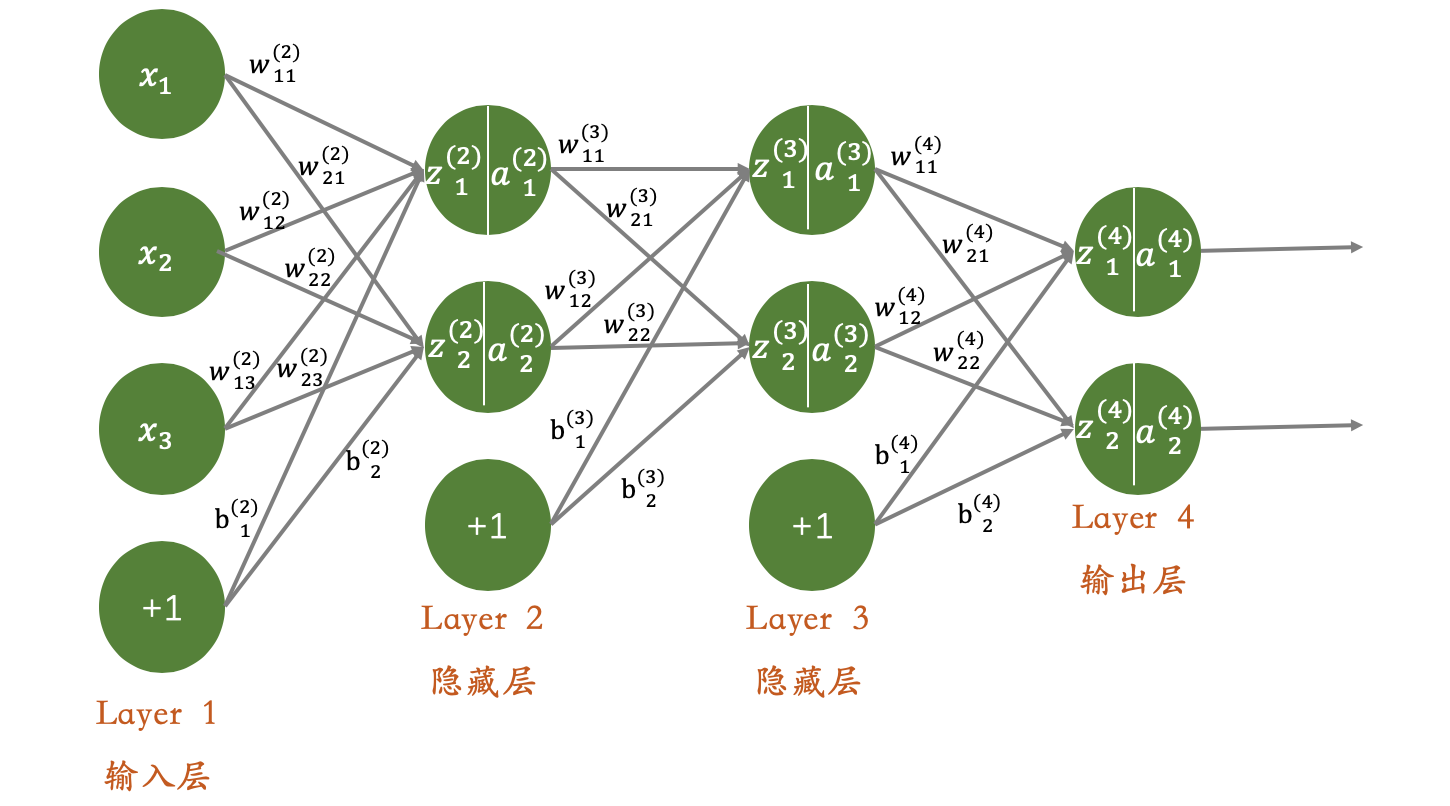
对于前向传播算法以及后向传播算法的介绍，我们将以如下的4层神经网络结构为例，进行介绍：

假设输入的样本为：
$x=(x1,x2,x3)T\mathbf{x}=(x_1,x_2,x_3)^T$
有两个隐藏层，分别为Layer 2、Layer 3，且输出结果为2维数据。

2.1前向传播算法

前向传播，也即正向传播，按照输入层、隐藏层到输出层的方向进行传播，即正向计算过程。

按照图例所示，我们可知：
$W(2)=[w11(2)w12(2)w13(2)w21(2)w22(2)w23(2)]W^{(2)}=\begin{bmatrix}w^{(2)}_{11}&w^{(2)}_{12}&w^{(2)}_{13} \\ w^{(2)}_{21}&w^{(2)}_{22}&w^{(2)}_{23}\\ \end{bmatrix}$
$W(3)=[w11(3)w12(3)w21(3)w22(3)]W^{(3)}=\begin{bmatrix}w^{(3)}_{11}&w^{(3)}_{12} \\ w^{(3)}_{21}&w^{(3)}_{22}&\\ \end{bmatrix}$
$b(2)=(b1(2),b2(2))Tb^{(2)}=(b^{(2)}_1,b^{(2)}_2)^T$
$b(3)=(b1(3),b2(3))Tb^{(3)}=(b^{(3)}_1,b^{(3)}_2)^T$
如果抛开矩阵运算，但从代数运算的过程来推到，我们可以轻易的得到：
Layer 2:
$z1(2)=x1w11(2)+x2w12(2)+x3w13(2)+b1(2)z_1^{(2)}=x_1w^{(2)}_{11}+x_2w^{(2)}_{12}+x_3w^{(2)}_{13}+b^{(2)}_1$
$z2(2)=x1w21(2)+x2w22(2)+x3w23(2)+b2(2)z_2^{(2)}=x_1w^{(2)}_{21}+x_2w^{(2)}_{22}+x_3w^{(2)}_{23}+b^{(2)}_2$
$a_1^{(2)}=f(z_1^{(2)})$
$a_2^{(2)}=f(z_2^{(2)})$
向量化对应的计算过程如下：
$(z1(2),z2(2))T=W(2)x+b(2)=[w11(2)w12(2)w13(2)w21(2)w22(2)w23(2)][x1x2x3]+[b1(2)b2(2)]=[x1w11(2)+x2w12(2)+x3w13(2)+b1(2)x1w21(2)+x2w22(2)+x3w23(2)+b2(2)]\begin{aligned}(z_1^{(2)},z_2^{(2)})^T&=W^{(2)}\mathbf{x}+b^{(2)}\\ &= \begin{bmatrix}w^{(2)}_{11}&w^{(2)}_{12}&w^{(2)}_{13} \\ w^{(2)}_{21}&w^{(2)}_{22}&w^{(2)}_{23} \end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}+\begin{bmatrix}b^{(2)}_1\\b^{(2)}_2\end{bmatrix} \\ &=\begin{bmatrix} x_1w^{(2)}_{11}+x_2w^{(2)}_{12}+x_3w^{(2)}_{13}+b^{(2)}_1\\ x_1w^{(2)}_{21}+x_2w^{(2)}_{22}+x_3w^{(2)}_{23}+b^{(2)}_2 \end{bmatrix} \end{aligned}$
$a^{(2)}=(f(z_1^{(2)}),f(z_2^{(2)}))^T$
Layer 3:
$z1(3)=a1(2)w11(3)+a2(2)w12(3)+b1(3)z_1^{(3)}=a_1^{(2)}w^{(3)}_{11}+a_2^{(2)}w^{(3)}_{12}+b^{(3)}_1$
$z2(3)=a1(2)w21(3)+a2(2)w22(3)+b2(3)z_2^{(3)}=a_1^{(2)}w^{(3)}_{21}+a_2^{(2)}w^{(3)}_{22}+b^{(3)}_2$
$a_1^{(3)}=f(z_1^{(3)})$
$a_2^{(3)}=f(z_2^{(3)})$
向量化对应的计算过程如下：
$(z1(3),z2(3))T=W(3)a(2)=[w11(3)w12(3)w21(3)w22(3)][a1(2)a2(2)]+[b1(3)b2(3)]=[a1(2)w11(3)+a2(2)w12(3)+b1(3)a1(2)w21(3)+a2(2)w22(3)+b2(3)]\begin{aligned}(z_1^{(3)},z_2^{(3)})^T&=W^{(3)}a^{(2)}\\ &=\begin{bmatrix}w^{(3)}_{11}&w^{(3)}_{12} \\ w^{(3)}_{21}&w^{(3)}_{22}&\\ \end{bmatrix}\begin{bmatrix}a^{(2)}_1\\a^{(2)}_2\end{bmatrix}+\begin{bmatrix}b^{(3)}_1\\b^{(3)}_2\end{bmatrix}\\ &=\begin{bmatrix} a_1^{(2)}w^{(3)}_{11}+a_2^{(2)}w^{(3)}_{12}+b^{(3)}_1\\ a_1^{(2)}w^{(3)}_{21}+a_2^{(2)}w^{(3)}_{22}+b^{(3)}_2 \end{bmatrix} \end{aligned}$
$a^{(3)}=(f(z_1^{(3)}),f(z_2^{(3)}))^T$
Layer 4:
$z1(4)=a1(3)w11(4)+a2(3)w12(4)+b1(4)z_1^{(4)}=a_1^{(3)}w^{(4)}_{11}+a_2^{(3)}w^{(4)}_{12}+b^{(4)}_1$
$z2(4)=a1(3)w21(4)+a2(3)w22(4)+b2(4)z_2^{(4)}=a_1^{(3)}w^{(4)}_{21}+a_2^{(3)}w^{(4)}_{22}+b^{(4)}_2$
$a_1^{(4)}=f(z_1^{(4)})$
$a_2^{(4)}=f(z_2^{(4)})$
向量化对应的计算过程如下：
$(z1(4),z2(4))T=W(4)a(3)=[w11(4)w12(4)w21(4)w22(4)][a1(3)a2(3)]+[b1(4)b2(4)]=[a1(3)w11(4)+a2(3)w12(4)+b1(4)a1(3)w21(4)+a2(3)w22(4)+b2(4)]\begin{aligned}(z_1^{(4)},z_2^{(4)})^T&=W^{(4)}a^{(3)}\\ &=\begin{bmatrix}w^{(4)}_{11}&w^{(4)}_{12} \\ w^{(4)}_{21}&w^{(4)}_{22}&\\ \end{bmatrix}\begin{bmatrix}a^{(3)}_1\\a^{(3)}_2\end{bmatrix}+\begin{bmatrix}b^{(4)}_1\\b^{(4)}_2\end{bmatrix}\\ &=\begin{bmatrix} a_1^{(3)}w^{(4)}_{11}+a_2^{(3)}w^{(4)}_{12}+b^{(4)}_1\\ a_1^{(3)}w^{(4)}_{21}+a_2^{(3)}w^{(4)}_{22}+b^{(4)}_2 \end{bmatrix} \end{aligned}$
$a^{(4)}=(f(z_1^{(4)}),f(z_2^{(4)}))^T$
我们将输入层的 $x_i$ 看做 $ai(1)a^{(1)}_i$ ,则可总结出以下结论：
第 $l(2≤l≤L)l(2\leq l \leq L)$ 层神经元的状态及激活值为：
$z^{(l)}=W^{(l)}a^{(l-1)}+b^{(l)}$
$a^{(l)}=f(z^{(l)})$
故前向传播算法的过程介绍完毕，即从输入一步一步的到达输出的传播过程。

2.2反向传播算法

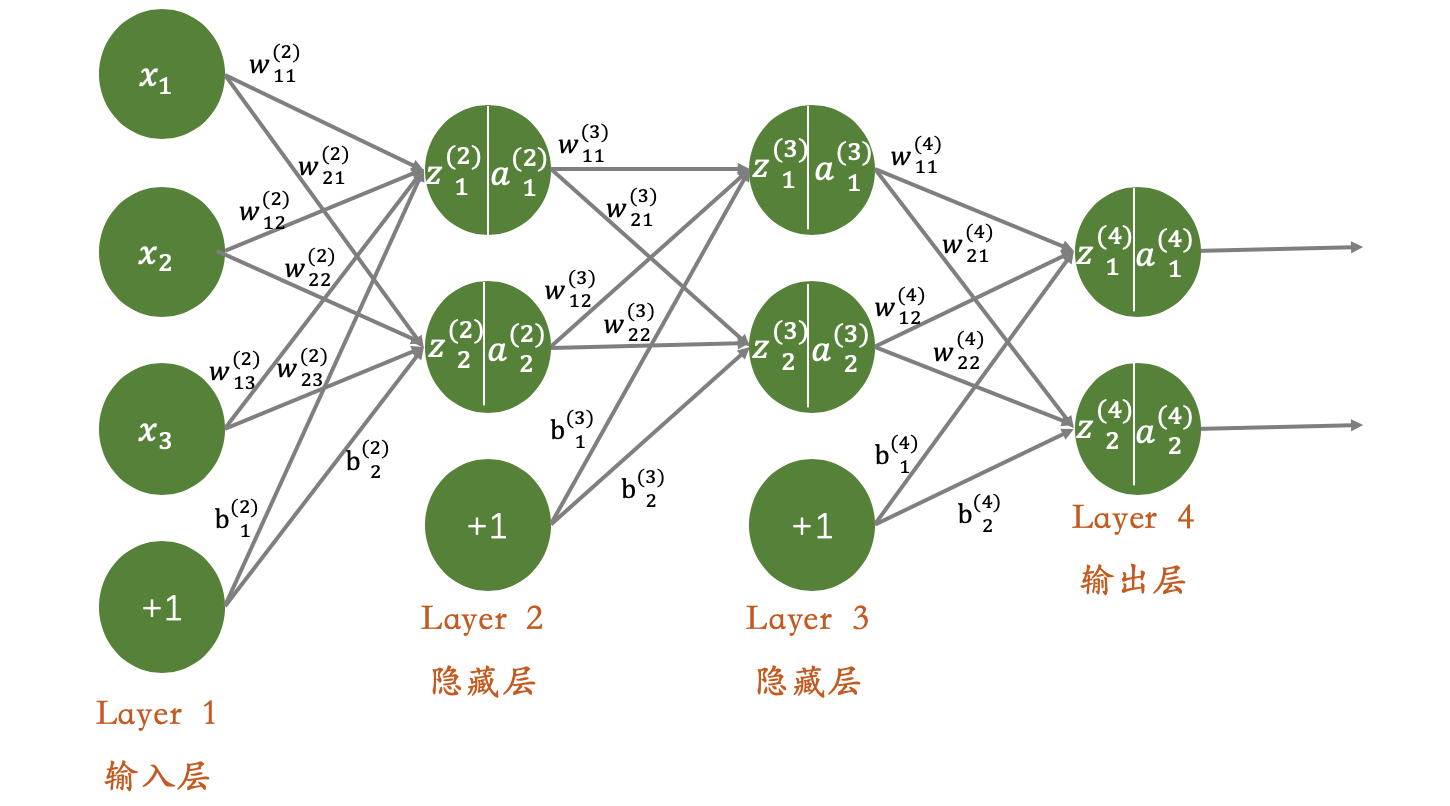
反向传播算法，其实和线性回归的思想是一样的，通过梯度下降的方法，逐渐调节参数，进而训练模型。所以此部分内容主要围绕梯度下降和误差反向传播来讲。关于梯度下降的具体细节，可以参考前面机器学习章节的线性回归内容。由于中间篇幅较长，为了便于阅读，再次将神经网络模型展示如下：

假设训练集样本为：
$T={(x(1),y(1)),(x(2),y(2)),⋯,(x(N),y(N))}T=\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots,(x^{(N)},y^{(N)})\}$
其中对应于上面的神经网络模型,则有：
$x(i)={x1(i),x2(i),x3(i)}x^{(i)}=\{x^{(i)}_1,x^{(i)}_2,x^{(i)}_3\}$
$y(i)={y1(i),y2(i)}y^{(i)}=\{y^{(i)}_1,y^{(i)}_2\}$
要对模型进行优化，则必须要有能够优化的函数。假设对于任一训练样本 $x^{(i)},y^{(i)})$ ,引入损失函数为：
$E(i)=12∣∣y(i)−o(i)∣∣=12∑k=1nL(yk(i)−ok(i))2E_{(i)}=\frac{1}{2}||y^{(i)}-o^{(i)}||=\frac{1}{2}\sum^{n_L}_{k=1}(y_k^{(i)}-o_k^{(i)})^2$
其中 $n_L$ 表示输入数据的维数，对于此处的模型而言 $n_L=3$ ； $y^{(i)}$ 代表样本的真实 $L a b e l$ ； $o^{(i)}$ 表示神经网络的输出结果。通过观察公式，我们不难发现，前面的系数 $12\frac{1}{2}$ 可有可无。此处加入该系数，只是为了后续计算(求导)方便。
根据损失函数，则整个神经网络的代价函数为：
$E(i)=12(y1(i)−a1(4))2+12(y2(i)−a2(4))=12(y1(i)−f(a1(3)w11(4)+a2(3)w12(4)+b1(4)))+12(y2(i)−f(a1(3)w21(4)+a2(3)w22(4)+b2(4))\begin{aligned}E_{(i)}&=\frac{1}{2}(y^{(i)}_1-a_1^{(4)})^2+\frac{1}{2}(y_2^{(i)}-a_2^{(4)})\\ &=\frac{1}{2}\left(y^{(i)}_1-f(a_1^{(3)}w^{(4)}_{11}+a_2^{(3)}w^{(4)}_{12}+b^{(4)}_1)\right)+\frac{1}{2}\left(y^{(i)}_2-f(a_1^{(3)}w^{(4)}_{21}+a_2^{(3)}w^{(4)}_{22}+b^{(4)}_2\right) \end{aligned}$
我们还可以进一步的展开，消去 $a1(3),a2(3)a^{(3)}_1,a^{(3)}_2$ ,直至公式中只含有权重参数、偏置参数、输入等。故通过反向传播，调整权重矩阵 $W^{(l)}$ 和偏置向量 $b^{(l)}$ 能够达到降低损失函数的目的。

算法推导
所有训练数据的总体（平均）代价可写成：
$Etotal=1N∑i=1NE(i)E_{total}=\frac{1}{N}\sum_{i=1}^NE_{(i)}$
当然我们的目标也是：调整权重和偏置试整体代价（误差）最小。
如果采用梯度下降法（或批量梯度下降法），即：
$W(l)=W(l)−μ∂Etotal∂W(l)=W(l)−μN∑i−1N∂E(i)∂W(l)\begin{aligned}W^{(l)}&=W^{(l)}-\mu \frac{\partial E_{total}}{\partial W^{(l)}}\\ &=W^{(l)}-\frac{\mu}{N}\sum_{i-1}^N\frac{\partial E_{(i)}}{\partial W^{(l)}} \end{aligned}$
$b(l)=b(l)−μ∂Etotal∂b(l)=b(l)−μN∑i−1N∂E(i)∂b(l)\begin{aligned}b^{(l)}&=b^{(l)}-\mu \frac{\partial E_{total}}{\partial b^{(l)}}\\ &=b^{(l)}-\frac{\mu}{N}\sum_{i-1}^N\frac{\partial E_{(i)}}{\partial b^{(l)}} \end{aligned}$
去更新参数 $W^{(l)},b^{(l)}$ 。由上面公式可知，秩序求得每个训练数据的代价函数 $E_{(i)}$ 对参数的偏导数 $∂E(i)∂W(l),∂E(i)∂b(l)\frac{\partial E_{(i)}}{\partial W^{(l)}},\frac{\partial E_{(i)}}{\partial b^{(l)}}$ ,即可进行参数的迭代更新。

我们以单个训练样本 $(x,y)(\mathbf{x},y)$ 为例，神经网络依然采用本文涉及的神经网络进行介绍，假设:
$x=(x1,x2,x3)Ty=(y1,y2)T\mathbf{x}=(x_1,x_2,x_3)^T \qquad \qquad \mathbf{y}=(y_1,y_2)^T$
逐层更新神经网络的权重参数 $W^{(l)}$ 。
首先更新输出层Layer 4权重参数，其损失函数表示为：
$E=12∣∣y−o∣∣=12((y1−a1(4))2+(y2−a2(4))2)=12((y1−f(z1(4)))2+(y2−f(z2(4)))2)=12((y1−f(a1(3)w11(4)+a2(3)w12(4)+b1(4)))2+(y2−f(a1(3)w21(4)+a2(3)w22(4)+b2(4)))2)\begin{aligned}E&=\frac{1}{2}||y-o|| \\ &=\frac{1}{2}\left((y_1-a^{(4)}_1)^2+(y_2-a^{(4)}_2)^2\right)\\ &=\frac{1}{2}\left( (y_1-f(z^{(4)}_1))^2+(y_2-f(z^{(4)}_2))^2 \right)\\ &=\frac{1}{2}\left( (y_1-f(a_1^{(3)}w^{(4)}_{11}+a_2^{(3)}w^{(4)}_{12}+b^{(4)}_1))^2+(y_2-f(a_1^{(3)}w^{(4)}_{21}+a_2^{(3)}w^{(4)}_{22}+b^{(4)}_2))^2 \right) \end{aligned}$
我们对Layer 4层的权重参数进行求偏导，以 $w11(4)w^{(4)}_{11}$ 为例，根据链式求导法则（复合函数求导法则）有：
$∂E∂w11(4)=12⋅2(y1−a1(4))(−∂a1(4)∂w11(4))=−(y1−a1(4))f′(z1(4))∂z1(4)∂w11(4)=−(y1−a1(4))f′(z1(4))a1(3)\begin{aligned} \frac{\partial E}{\partial w^{(4)}_{11}}&=\frac{1}{2}\cdot 2\left(y_1-a^{(4)}_1\right)\left(-\frac{\partial a^{(4)}_1}{\partial w^{(4)}_{11}}\right)\\ &=-\left(y_1-a^{(4)}_1\right)f'(z_1^{(4)})\frac{\partial z_1^{(4)}}{\partial w^{(4)}_{11}}\\ &=-\left(y_1-a^{(4)}_1\right)f'(z_1^{(4)})a^{(3)}_1 \end{aligned}$
如果我们记： $∂E∂zi(l)=δi(l)\frac{\partial E}{\partial z_i^{(l)}}=\delta^{(l)}_i$
则可以得到如下变换：
$∂E∂w11(4)=∂E∂z1(4)∂z1(4)∂w11(4)=δ1(4)a1(3)\begin{aligned}\frac{\partial E}{\partial w^{(4)}_{11}} &=\frac{\partial E}{\partial z_1^{(4)}} \frac{\partial z_1^{(4)}}{\partial w^{(4)}_{11}}\\ &=\delta^{(4)}_1a^{(3)}_1 \end{aligned}$
其中： $δ1(4)=∂E∂z1(4)=−(y1−a1(4))f′(z1(4))\delta^{(4)}_1=\frac{\partial E}{\partial z^{(4)}_1}=-\left(y_1-a^{(4)}_1\right)f'(z_1^{(4)})$
同理可求得其余的权重参数：
$∂E∂w12(4)=δ1(4)a2(3)\frac{\partial E}{\partial w^{(4)}_{12}}=\delta^{(4)}_1 a^{(3)}_2$
$∂E∂w21(4)=δ2(4)a1(3)\frac{\partial E}{\partial w^{(4)}_{21}}=\delta^{(4)}_2 a^{(3)}_1$
$∂E∂w22(4)=δ2(4)a2(3)\frac{\partial E}{\partial w^{(4)}_{22}}=\delta^{(4)}_2 a^{(3)}_2$
其中 $δ2(4)=−(y2−a2(4))f′(z2(4))\delta^{(4)}_2=-(y_2-a^{(4)}_2)f'(z^{(4)}_2)$
推广到一般情况，假设神经网络共 $L$ 层，则：
$δi(L)=−(yi−ai(L))f′(zi(L))1≤i≤nL\delta^{(L)}_i=-(y_i-a^{(L)}_i)f'(z_i^{(L)}) \qquad\qquad 1\leq i\leq n_L$
$∂E∂wij(L)=δi(L)aj(L−1)1≤i≤nL,1≤j≤nL−1\frac{\partial E}{\partial w_{ij}^{(L)}}=\delta_i^{(L)}a_j^{(L-1)} \qquad\qquad 1 \leq i \leq n_L,1\leq j \leq n_{L-1}$
如果把上面的两个公式表达为矩阵，则为：
$δ(L)=−(y−a(L))⨀f′(z(L))\delta^{(L)}=-(y-a^{(L)})\bigodot f'(z^{(L)})$
$▽W(L)E=δ(L)(a(L−1))T\bigtriangledown_{W^{(L)}}E=\delta^{(L)}(a^{(L-1)})^T$
其中 $⨀\bigodot$ 表示矩阵对应位置相乘。
其次,隐藏层Layer 3的权重参数更新
在介绍更新之前，很有必要进行一个相关的推导，根据 $δi(l)\delta_i^{(l)}$ 的定义：
$∂E∂wij(l)=∂E∂zi(l)∂zi(l)∂wij(l)=δi(l)∂zi(l)∂wij(l)=δi(l)aj(l−1)\begin{aligned} \frac{\partial E}{\partial w^{(l)}_{ij}}&=\frac{\partial E}{\partial z^{(l)}_i}\frac{\partial z^{(l)}_i}{\partial w^{(l)}_{ij}}\\ &=\delta^{(l)}_i\frac{\partial z^{(l)}_i}{\partial w^{(l)}_{ij}}\\ &=\delta^{(l)}_i a_j^{(l-1)} \end{aligned}$
并且，
$δi(l)=∂E∂zi(l)=∑j=1nl+1∂E∂zj(l+1)∂zj(l+1)∂zi(l)=∑j=1nl+1δj(l+1)∂zj(l+1)∂zi(l)⋯(1)\begin{aligned} \delta_i^{(l)}&=\frac{\partial E}{\partial z_i^{(l)}}\\ &=\sum_{j=1}^{n_{l+1}}\frac{\partial E}{\partial z_j^{(l+1)}}\frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}}\\ &=\sum_{j=1}^{n_{l+1}}\delta_j^{(l+1)}\frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}} \qquad\qquad \cdots(1) \end{aligned}$

疑问： $δi(l)=∑j=1nl+1∂E∂zj(l+1)∂zj(l+1)∂zi(l)\delta_i^{(l)}=\sum_{j=1}^{n_{l+1}}\frac{\partial E}{\partial z_j^{(l+1)}}\frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}}$ 如何推导？
因为 $l + 1$ 层的每个神经元均和 $l$ 层的 $z_i^{(l)}$ 神经元相连，所以在函数 $E$ 中，自变量 $z_i^{(l)}$ 出现了 $n_{l+1}$ 次，出现的每一次均对应一个 $zj(l+1),1≤j≤nl+1z_j^{(l+1)},1\leq j\leq n_{l+1}$ 。从而由“函数之和的求导法则”及“求导的链式法则”有：
$∂E∂zi(l)=∂E∂z1(l+1)∂z1(l+1)∂zi(l)+∂E∂z2(l+1)∂z2(l+1)∂zi(l)+⋯+∂E∂znl+1(l+1)∂znl+1(l+1)∂zi(l)=∑j=1nl+1∂E∂zj(l+1)∂zj(l+1)∂zi(l)\begin{aligned} \frac{\partial E}{\partial z_i^{(l)}}&=\frac{\partial E}{\partial z_1^{(l+1)}}\frac{\partial z_1^{(l+1)}}{\partial z_i^{(l)}}+\frac{\partial E}{\partial z_2^{(l+1)}}\frac{\partial z_2^{(l+1)}}{\partial z_i^{(l)}}+\cdots+\frac{\partial E}{\partial z_{n_{l+1}}^{(l+1)}}\frac{\partial z_{n_{l+1}}^{(l+1)}}{\partial z_i^{(l)}}\\ &=\sum_{j=1}^{n_{l+1}}\frac{\partial E}{\partial z_j^{(l+1)}}\frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}}\end{aligned}$
详情参考：BP 算法原理和详细推导流程

对上式(1)继续化简，由于：
$zj(l+1)=∑i=1nlwij(l+1)ai(l)+bj(l+1)=∑i=1nlwij(l+1)f(zi(l))+bj(l+1)z_j^{(l+1)}=\sum_{i=1}^{n_l}w_{ij}^{(l+1)}a_i^{(l)}+b^{(l+1)}_j=\sum_{i=1}^{n_l}w_{ij}^{(l+1)}f(z_i^{(l)})+b^{(l+1)}_j$
故有：
$∂zj(l+1)∂zi(l)=∂zj(l+1)∂ai(l)∂ai(l)∂zi(l)=wji(l+1)f′(zi(l))⋯(2)\frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}}=\frac{\partial z_j^{(l+1)}}{\partial a_i^{(l)}}\frac{\partial a_i^{(l)}}{\partial z_i^{(l)}}=w_{ji}^{(l+1)}f'(z_i^{(l)}) \qquad\qquad \cdots (2)$
联立（1）（2）两式可得：

$δi(l)=∑j=1nl+1δj(l+1)∂zj(l+1)∂zi(l)=∑j=1nl+1δj(l+1)wji(l+1)f′(zi(l))=(∑j=1nl+1δj(l+1)wji(l+1))f′(zi(l))\begin{aligned} \delta_i^{(l)}&=\sum_{j=1}^{n_{l+1}}\delta_j^{(l+1)}\frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}}\\ &=\sum_{j=1}^{n_{l+1}}\delta_j^{(l+1)}w_{ji}^{(l+1)}f'(z_i^{(l)})\\ &=\left(\sum_{j=1}^{n_{l+1}}\delta_j^{(l+1)}w_{ji}^{(l+1)}\right)f'(z_i^{(l)}) \end{aligned}$

故此刻，BP算法最重要的公式已经证明完毕，它利用 $l + 1$ 层的 $δ(l+1)\delta^{(l+1)}$ 来计算 $l$ 层的 $δ(l)\delta^{(l)}$ ，这就是“误差反向传播算法”名字的由来。如果把它表达为矩阵(向量)形式，则为:

$δ(l)=((W(l+1))Tδ(l+1))⨀f′(zi(l))\delta^{(l)}=\left((W^{(l+1)})^T\delta^{(l+1)}\right)\bigodot f'(z_i^{(l)})$

通过以上证明，此刻我们回到Layer 3层的参数更新：
由以上公式我们可得：
$∂E∂wij(l)=δi(l)aj(l−1)=(∑j=1nl+1δj(l+1)wji(l+1))f′(zi(l))aj(l−1)\begin{aligned} \frac{\partial E}{\partial w^{(l)}_{ij}}&=\delta^{(l)}_i a_j^{(l-1)}\\ &=\left(\sum_{j=1}^{n_{l+1}}\delta_j^{(l+1)}w_{ji}^{(l+1)}\right)f'(z_i^{(l)})a_j^{(l-1)} \end{aligned}$
故Layer 3 各参数权重为：
$∂E∂w11(3)=(δ1(4)w11(4)+δ2(4)w21(4))f′(z1(3))a1(2)\frac{\partial E}{\partial w_{11}^{(3)}}=(\delta^{(4)}_1w_{11}^{(4)}+\delta^{(4)}_2w_{21}^{(4)})f'(z_1^{(3)})a_1^{(2)}$
$∂E∂w12(3)=(δ1(4)w11(4)+δ2(4)w21(4))f′(z1(3))a2(2)\frac{\partial E}{\partial w_{12}^{(3)}}=(\delta^{(4)}_1w_{11}^{(4)}+\delta^{(4)}_2w_{21}^{(4)})f'(z_1^{(3)})a_2^{(2)}$
$∂E∂w21(3)=(δ1(4)w12(4)+δ2(4)w22(4))f′(z2(3))a1(2)\frac{\partial E}{\partial w_{21}^{(3)}}=(\delta^{(4)}_1w_{12}^{(4)}+\delta^{(4)}_2w_{22}^{(4)})f'(z_2^{(3)})a_1^{(2)}$
$∂E∂w22(3)=(δ1(4)w12(4)+δ2(4)w22(4))f′(z2(3))a2(2)\frac{\partial E}{\partial w_{22}^{(3)}}=(\delta^{(4)}_1w_{12}^{(4)}+\delta^{(4)}_2w_{22}^{(4)})f'(z_2^{(3)})a_2^{(2)}$
最后，更新隐藏层Layer 2 的权重参数，同样根据：
$∂E∂wij(l)=(∑j=1nl+1δj(l+1)wji(l+1))f′(zi(l))aj(l−1)\frac{\partial E}{\partial w^{(l)}_{ij}}=\left(\sum_{j=1}^{n_{l+1}}\delta_j^{(l+1)}w_{ji}^{(l+1)}\right)f'(z_i^{(l)})a_j^{(l-1)}$
此处省略参数更新的具体细节。
除了更新权重参数以外，我们公式中还包含有偏置参数 $b$ ,更新偏置参数 $b$ 如下：
$∂E∂bi(l)=∂E∂zi(l)∂zi(l)∂bi(l)=δi(l)\frac{\partial E}{\partial b_i^{(l)}}=\frac{\partial E}{\partial z_i^{(l)}}\frac{\partial z_i^{(l)}}{\partial b_i^{(l)}}=\delta_i^{(l)}$
向量化为：
$▽b(l)E=δ(l)\bigtriangledown_{b^{(l)}}E=\mathbf{\delta^{(l)}}$

3.核心公式汇总

$δi(L)=−(yi−ai(L))f′(zi(L))1≤i≤nL\delta^{(L)}_i=-(y_i-a^{(L)}_i)f'(z_i^{(L)}) \qquad\qquad 1\leq i\leq n_L$
$δi(l)=(∑j=1nl+1δj(l+1)wji(l+1))f′(zi(l))\delta_i^{(l)}=\left(\sum_{j=1}^{n_{l+1}}\delta_j^{(l+1)}w_{ji}^{(l+1)}\right)f'(z_i^{(l)})$
$∂E∂wij(l)=δi(l)aj(l−1)\frac{\partial E}{\partial w^{(l)}_{ij}}=\delta^{(l)}_i a_j^{(l-1)}$
$∂E∂bi(l)=δi(l)\frac{\partial E}{\partial b_i^{(l)}}=\delta_i^{(l)}$
向量化对应的公式为：
$δ(L)=−(y−a(L))⨀f′(z(L))\delta^{(L)}=-(y-a^{(L)})\bigodot f'(z^{(L)})$
$δ(l)=((W(l+1))Tδ(l+1))⨀f′(zi(l))\delta^{(l)}=\left((W^{(l+1)})^T\delta^{(l+1)}\right)\bigodot f'(z_i^{(l)})$
$▽W(L)E=δ(L)(a(L−1))T\bigtriangledown_{W^{(L)}}E=\delta^{(L)}(a^{(L-1)})^T$
$▽b(l)E=δ(l)\bigtriangledown_{b^{(l)}}E=\mathbf{\delta^{(l)}}$

4.算法实现流程

借助于以上的四个核心公式，我们可以归纳BP算法的具体流程

4.1 单个训练样本的BP算法流程

初始化参数 $W,b\mathbf{W,b}$
一般地，把 $wij(l),bi(l),2≤l≤Lw_{ij}^{(l)},b_i^{(l)},2\leq l\leq L$ 初始化为一个很小的，接近于零的随机值。

注意:不要把 $wij(l),bi(l),2≤l≤Lw_{ij}^{(l)},b_i^{(l)},2\leq l\leq L$ 全部初始化为零或者相同的其它值，这会导致对于所有 $i$ ， $w_{ij}^{(l)}$ 都会取相同的值。
利用下面的“前向传播”公式计算每层的状态和激活值:
$z^{(l)}=W^{(l)}a^{(l-1)}+b^{(l)}$
$a^{(l)}=f(z^{(l)})$
计算 δ(l)
首先，利用下面公式计算输出层的 $δ(L)\delta^{(L)}$
$δi(L)=−(yi−ai(L))f′(zi(L))1≤i≤nL\delta^{(L)}_i=-(y_i-a^{(L)}_i)f'(z_i^{(L)}) \qquad\qquad 1\leq i \leq n_L$
其中， $y_i$ 是期望的输出(这是训练数据给出的已知值)， $a_i^{(L)}$ 是神经网络对训练数据产生的实际输出。然后，利用下面公式从第 $L - 1$ 层到第 2 层依次计算隐藏层的 $δ(l),(l=L−1,L−2,L−3,⋯,2)\delta^{(l)},(l = L-1,L-2,L-3,\cdots ,2)$
$δi(l)=(∑j=1nl+1δj(l+1)wji(l+1))f′(zi(l))\delta_i^{(l)}=\left(\sum_{j=1}^{n_{l+1}}\delta_j^{(l+1)}w_{ji}^{(l+1)}\right)f'(z_i^{(l)})$
按下面公式求这个训练数据的代价函数对参数的偏导数:
$∂E∂wij(l)=δi(l)aj(l−1)\frac{\partial E}{\partial w^{(l)}_{ij}}=\delta^{(l)}_i a_j^{(l-1)}$
$∂E∂bi(l)=δi(l)\frac{\partial E}{\partial b_i^{(l)}}=\delta_i^{(l)}$

4.2BP“批量梯度下降”算法总结

用 BP 算法四个核心公式求得每一个训练数据的代价函数对参数的偏导数;
按下面公式更新参数:
$W(l)=W(l)−μN∑i=1N∂E(i)∂W(l)W^{(l)}=W^{(l)}-\frac{\mu}{N}\sum_{i=1}^N\frac{\partial E_{(i)}}{\partial W^{(l)}}$
$b(l)=b(l)−μN∑i=1N∂E(i)∂b(l)b^{(l)}=b^{(l)}-\frac{\mu}{N}\sum_{i=1}^N\frac{\partial E_{(i)}}{\partial b^{(l)}}$
迭代执行第 (1),(2) 步，直到满足停止准则(比如相邻两次迭代的误差的差别很小，或者直接限制迭代的次数)。

说明:每对参数进行一次更新都要遍历整个训练数据集，当训练数据集不大时这不是问题，当训练数据集非常巨大时，可以采用随机梯度下降法(每次仅使用一个训练数据来更新参数)。

参考文献

BP 算法原理和详细推导流程

热搜

最近搜索清空