机器学习100天——实现简单线性回归(第二天)

线性回归算法的作用是使用单一特征来预测响应值。是一种根据自变量X预测因变量Y的方法。假设两个变量是线性相关的，那么我们要找到一个线性函数，根据特征或自变量X来精确预测响应值Y。

如何找到最佳拟合线

在这个回归模型中，我们尝试通过寻找最佳拟合线来最小化预测的误差——根据线性回归预测的结果误差最小。我们尝试最小化观察值和预测值之间的长度，长度越小，误差就越小，反之亦然。

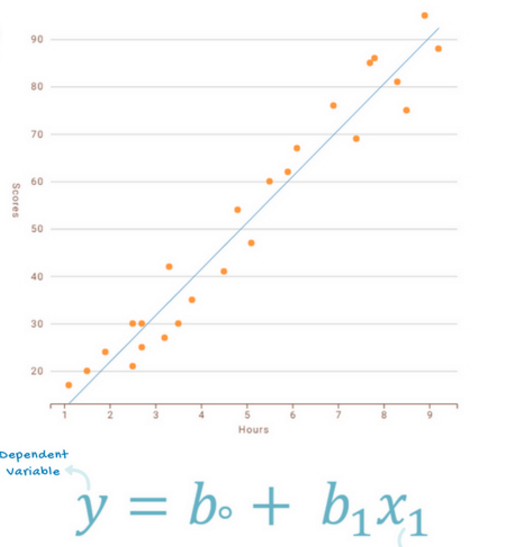
我们将使用一个根据学生花费在学习上的小时数预测他们分数的百分比的例子学习如何使用线性回归模型。请看下图：

线性回归模型为：
y=b0+b1x1y=b0+b1x1
将上图中的自变量和因变量代入到上面的模型中，则变为：
Score=b0+b1∗hoursScore=b0+b1∗hours

线性回归其实就是解一元一次方程，求出截距和斜率。

下面介绍使用Python实现线性回归算法的步骤。
步骤1：数据预处理

• 导入相关库

• 导入数据集

• 检查缺失数据

• 划分数据集

• 使用简单线性回归模型进行特征缩放

步骤2：通过训练集来训练简单线性回归模型
为了使用模型来训练数据集，我们将使用来自sklern.liner_model库的LinearRegression类，然后创建一个LinearRegression类对象regressor，最后使用该对象的fit()方法对数据集进行训练。

步骤3：预测结果
现在我们将预测来自训练集的观察结果。我们将把输出保存在向量Y_pred中。我们使用前一步中训练的回归模型regressor的LinearGression类的预测方法来对结果进行预测。

步骤4：预测结果可视化
使用matplotlib.pyplot库对我们的训练结果和测试结果做散点图，以查看我们的模型预测效果。

具体实现代码如下：
第一步：数据预处理

import pandas as pd  
import numpy as np  
import matplotlib.pyplot as plt  

dataset = pd.read_csv('studentscores.csv')  
X = dataset.iloc[ : ,   : 1 ].values  
Y = dataset.iloc[ : , 1 ].values  

from sklearn.model_selection import train_test_split  
X_train, X_test, Y_train, Y_test = train_test_split( X, Y, test_size = 1/4, random_state = 0)

第二步：通过训练集来训练简单线性回归模型

from sklearn.linear_model import LinearRegression  
regressor = LinearRegression()  
regressor = regressor.fit(X_train, Y_train)

第三步：预测结果

Y_pred = regressor.predict(X_test)

第四步：可视化
训练结果可视化：

plt.scatter(X_train , Y_train, color = 'red')  
plt.plot(X_train , regressor.predict(X_train), color ='blue')  
plt.show()

测试结果可视化：

plt.scatter(X_test , Y_test, color = 'red')  
plt.plot(X_test , regressor.predict(X_test), color ='blue')  
plt.show()

作者：Summer哥 
出处：https://www.cnblogs.com/airnew/p/9758241.html