javaScript 赌运气的四舍五入
javaScript 赌运气的四舍五入
起源于线上一个BUG,计算值与后端java 的 BigDecimal计算值不匹配,追踪数据,在tofixed 和 round 的时候数据不精准
10.135.toFixed(2) //10.131
这就很不友好了啊,想一下解决方案,首先 先要知道为啥
如果参数的小数部分恰好等于0.5,则舍入到下一个在正无穷(+∞)方向上的整数。注意,与很多其他语言中的round()函数不同,Math.round()并不总是舍入到远离0的方向(尤其是在负数的小数部分恰好等于0.5的情况下)–MDN
这种情势是为啥呢,有经验的都知道 ,肯定是进制的锅了啊
先看一下储存结构
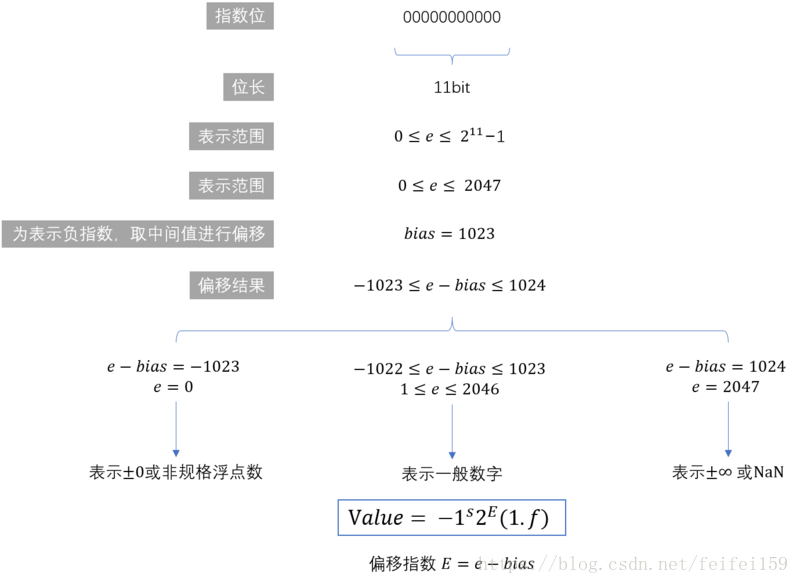
ECMA-262 遵循 IEEE 754 规范,采用双精度存储(double precision),占用 64 bit 
存储结构中可以看出, 指数部分的长度是11个二进制,即指数部分能表示的最大值是 2047(211-1),取中间值进行偏移,用来表示负指数,也就是说指数的范围是 [-1023,1024] 。因此,这种存储结构能够表示的数值范围为 21024 到 2-1023 ,超出这个范围的数无法表示 。21024 转换为科学计数法如下所示:
21024 = 1.7976931348623157 × 103081
因此,JavaScript 中能表示的最大值是 1.7976931348623157e+308,最小值为 5e-324 。
这两个边界值可以分别通过访问 Number 对象的 MAX_VALUE 属性和 MIN_VALUE 属性来获取:
Number.MAX_VALUE; //1.7976931348623157e+308 Number.MIN_VALUE; //5e-324
如果数字超过最大值或最小值,JavaScript 将返回一个不正确的值,这称为正向溢出(overflow) 或 负向溢出(underflow) 。
Number.MAX_VALUE+1 == Number.MAX_VALUE; //true Number.MAX_VALUE+1e292; //Infinity Number.MIN_VALUE + 1; //1 Number.MIN_VALUE - 3e-324; //0 Number.MIN_VALUE - 2e-324; //5e-324
然后数值精度就知道了
在 64 位的二进制中,符号位决定了一个数的正负,指数部分决定了数值的大小,小数部分决定了数值的精度。
IEEE754 规定,有效数字第一位默认总是1 。因此,在表示精度的尾数前面,还存在一个隐藏位 ,固定为 1 ,但它不保存在 64 位浮点数之中。也就是说,有效数字总是 1.xx…xx 的形式,其中 xx..xx 的部分保存在 64 位浮点数之中,最长为52位 。所以,JavaScript 提供的有效数字最长为 53 个二进制位,其内部实际的表现形式为:
(-1)^符号位 * 1.xx…xx * 2^指数位
这意味着,JavaScript 能表示并进行精确算术运算的整数范围为:[-253-1,253-1],即从最小值 -9007199254740991 到最大值 9007199254740991 之间的范围 。
Math.pow(2, 53)-1 ; // 9007199254740991 -Math.pow(2, 53)-1 ; // -9007199254740991
可以通过 Number.MAX_SAFE_INTEGER 和 Number.MIN_SAFE_INTEGER 来分别获取这个最大值和最小值。
console.log(Number.MAX_SAFE_INTEGER) ; // 9007199254740991 console.log(Number.MIN_SAFE_INTEGER) ; // -9007199254740991
对于超过这个范围的整数,JavaScript 依旧可以进行运算,但却不保证运算结果的精度。
Math.pow(2, 53) ; // 9007199254740992 Math.pow(2, 53) + 1; // 9007199254740992 9007199254740993; //9007199254740992 90071992547409921; //90071992547409920 0.923456789012345678;//0.9234567890123456`
然后我们再看一下为啥会精度丢失
计算机中的数字都是以二进制存储的,如果要计算 0.1 + 0.2 的结果,计算机会先把 0.1 和 0.2 分别转化成二进制,然后相加,最后再把相加得到的结果转为十进制 。
但有一些浮点数在转化为二进制时,会出现无限循环 。比如, 十进制的 0.1 转化为二进制,会得到如下结果:
0.0001 1001 1001 1001 1001 1001 1001 1001 …(1001无限循环) 1
而存储结构中的尾数部分最多只能表示 53 位。为了能表示 0.1,只能模仿十进制进行四舍五入了,但二进制只有 0 和 1 , 于是变为 0 舍 1 入 。 因此,0.1 在计算机里的二进制表示形式如下:
0.00011001100110011001100110011001100110011001100110011011
用标准计数法表示如下:
(−1)0 × 2−4 × (1.1001100110011001100110011001100110011001100110011010)21
同样,0.2 的二进制也可以表示为:
(−1)0 × 2−3 × (1.1001100110011001100110011001100110011001100110011010)2 1
在计算浮点数相加时,需要先进行对位,将较小的指数化为较大的指数,并将小数部分相应右移:
0.1 (−1)0 × 2−3 × (0.11001100110011001100110011001100110011001100110011010)2 0.2 (−1)0 × 2−3 × (1.1001100110011001100110011001100110011001100110011010)212
最终,0.1 + 0.2 在计算机里的计算过程如下:
经过上面的计算过程,0.1 + 0.2 得到的结果也可以表示为:
(−1)0 × 2−2 × (1.0011001100110011001100110011001100110011001100110100)21
然后,通过 JS 将这个二进制结果转化为十进制表示:
(-1)**0 * 2**-2 * (0b10011001100110011001100110011001100110011001100110100 * 2**-52); //0.30000000000000004 console.log(0.1 + 0.2) ; // 0.30000000000000004
这是一个典型的精度丢失案例,从上面的计算过程可以看出,0.1 和 0.2 在转换为二进制时就发生了一次精度丢失,而对于计算后的二进制又有一次精度丢失 。因此,得到的结果是不准确的。
2.5 特殊数值
JavaScript 提供了几个特殊数值,用于判断数字的边界和其他特性 。如下所示:
Number.MAX_VALUE:JavaScript 中的最大值 Number.MIN_VALUE:JavaScript 中的最小值 Number.MAX_SAFE_INTEGER:最大安全整数,为 253-1 Number.MIN_SAFE_INTEGER:最小安全整数,为 -(253-1) Number.POSITIVE_INFINITY:对应 Infinity,代表正无穷 Number.NEGATIVE_INFINITY:对应 -Infinity,代表负无穷 Number.EPSILON:是一个极小的值,用于检测计算结果是否在误差范围内 Number.NaN:表示非数字,NaN与任何值都不相等,包括NaN本身 Infinity:表示无穷大,分 正无穷 Infinity 和 负无穷 -Infinity
如何进行数值转换
有 3 个函数可以把非数值转换为数值: Number()、parseInt() 和 parseFloat()。Number() 可以用于任何数据类型,而另两个函数则专门用于把字符串转换成数值。
对于字符串而言,Number() 只能对字符串进行整体转换,而 parseInt() 和 parseFloat() 可以对字符串进行部分转换,即只转换第一个无效字符之前的字符。
对于不同数据类型的转换,Number() 的处理也不尽相同,其转换规则如下:
【1】如果是 Boolean 值,true 和 false 将分别被转换为 1 和 0。
【2】如果是数字值,只是简单的传入和返回。
【3】如果是 null 值,返回 0。
【4】如果是 undefined,返回 NaN。
【5】如果是字符串,遵循下列规则:
如果字符串中只包含数字(包括前面带正号或负号的情况),则将其转换为十进制数值;
如果字符串中包含有效的浮点格式,则将其转换为对应的浮点数值;
如果字符串中包含有效的十六进制格式,则将其转换为相同大小的十进制整数值;
如果字符串是空的(不包含任何字符),则将其转换为 0;
如果字符串中包含除上述格式之外的字符,则将其转换为 NaN。
【6】如果是对象,则调用对象的 valueOf() 方法,然后依照前面的规则转换返回的值。如果转换的结果是 NaN,则调用对象的 toString() 方法,然后再次依照前面的规则转换返回的字符串值。
注意:一元加操作符[+] 和 Number() 具有同样的作用。
速度更快精度更差的位运算
位操作符用于在最基本的层次上,即按内存中表示数值的位来操作数值。ECMAScript 中的所有数值都以 IEEE754 64 位格式存储,但位操作符并不直接操作 64 位的值。而是先将 64 位的值转换成 32 位的整数,然后执行操作,最后再将结果转换回 64 位。常见的位运算有以下几种:
按位非(NOT):~ 按位与(AND):& 按位或(OR): | 按位异或(XOR):^ 左移:<< 有符号右移:>> 无符号右移:>>>
四舍五入怎么才能好用
首先我们先看一下数据是怎么存的 ECMA-262 只需要最多 21 位显示数字。
0.135.toPrecision(21) //"10.1349999999999997868" 每个人可能不一样。。
问题到这里 基本就明了了,怎么解决呢,上代码。。
/**
* 四舍五入
* @param number 要四舍五入的数字
* @param precision 精度 保留小数点位数
* @returns {*}
*/
function round(number,precision) {
const enlargeDigits = function enlargeDigits(times) {
return function (number) {
return +(String(number) + "e" + String(times));
};
};
const toFixed = function toFixed(precision) {
return function (number) {
return number.toFixed(precision);
};
};
const compose = function compose() {
for (var _len = arguments.length, functions = Array(_len), _key = 0; _key < _len; _key++) {
functions[_key] = arguments[_key];
}
var nonFunctionTypeLength = functions.filter(function (item) {
return typeof item !== 'function';
}).length;
if (nonFunctionTypeLength > 0) {
throw new Error("compose's params must be functions");
}
if (functions.length === 0) {
return function (arg) {
return arg;
};
}
if (functions.length === 1) {
return functions[0];
}
return functions.reduce(function (a, b) {
return function () {
return a(b.apply(undefined, arguments));
};
});
};
var precision = arguments.length > 1 && arguments[1] !== undefined ? arguments[1] : 2;
if (Number.isNaN(+number)) {
throw new Error("number's type must be Number");
}
if (Number.isNaN(+precision)) {
throw new Error("precision's type must be Number");
}
return compose(toFixed(precision), enlargeDigits(-precision), Math.round, enlargeDigits(precision))(number)
}共同学习,写下你的评论
评论加载中...
作者其他优质文章