title: 数据结构之图的关键路径
tags: 数据结构与算法之美

一、AOE和AOV网

1.AOE网

AOE-网指用边表示活动的网是一个带权的有向无环图其中顶点表示事件弧表示活动权表示活动持续的时间通常一个AOE-网可用来估算工程的完成时间。

AOE网具有以下几个性质

(1) 只有在某顶点所代表的事件发生后从该顶点出发的各有向边所代表的活动才能开始

(2) 只有在进入某一顶点的各有向边所代表的活动都已经结束该顶点所代表的事件才能发生

(3) 表示实际工程计划的AOE网应该是无环的并且存在惟一的入度过为0的开始顶点(源点和惟一的出度为0的完成顶点汇点。

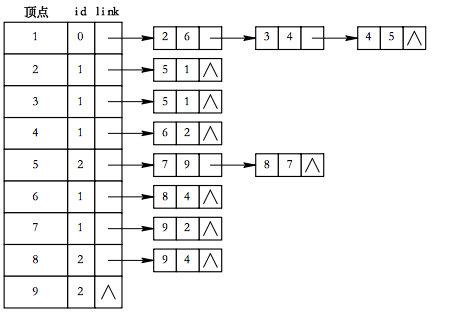
对于AOE-网我们不妨采用与AOV-网一样的邻接表的存储方式其中邻接表中边结点增设一个dut域存放该边的权值即该有向边代表的活动所持续的时间。

下图给出了上图所示的AOE-网的邻接表。

如果用AOE网来表示一项工程那么仅仅考虑各个子工程之间的优先关系还不够更多的是关心整个工程完成的最短时间是多少哪些活动的延迟将会影响整个工程的进度而加速这些活动又能导致提高整个工程的效率。因此对AOE网有待研究的问题是:

(1) 完成整个工程至少需要多少时间

(2) 哪些活动是影响工程进度的关键。

二、关键路径

由于在AOE-网中某些活动可以并行地进行因此完成工程的最短时间是从开始顶点源点到完成顶点汇点的最大路径长度这里所说的路径的长度等于这条路径上完成各个活动所需时间之和不是路径上弧的数目;
具有最大路径长度的路径称为关键路径。

为了寻找关键活动确定关键路径我们先定义几个变量

(1)事件的最早发生时间ve(i)从v1到vi的最长路径长度。

(2)事件的最迟发生时间vl(i)完成顶点vn的最早发生时间ve(n)减去vi到vn的最长路径长度。

(3)活动ai的最早开始时间e(i)事件vj的最早发生时间ve(j)也是所有以vj为起点的出边< vj, vk>所表示的活动ai的最早开始的时间即e(i)=ve(j)。

(4)活动的最迟开始时间l(i)是ai的最迟完成时间减去ai的持续时间即l(i)=vl(k)-< vj , vk>的权。
通常把e(i)=l(i)的活动称为关键活动

由上述分析可知若把所有活动ai的最早开始时间e(i)和最迟开始时间l(i)都计算出来即可找到所有的关键活动。为了求得AOE网的e(i)和l(i)应该先求得网中所有事件vj的最早发生时间ve(j)和最迟发生时间vl(j)。若活动ai由边<vj, vk>表示其持续时间记为dut(<j, k>)则有如下关系

e(i)=ve(j)
l(i)=vl(k)-dut(<j, k>)

求关键路径的算法描述

1) 根据有向网的弧建立图的邻接表作存储结构

2) 从源点v0出发令ve[0]=0,按拓扑序列求各顶点的ve[i]

3) 从汇点vn-1出发令vl[n-1]=ve[n-1],按逆拓扑序列求其余各顶点的vl[i]

4) 根据各顶点的ve和vl值计算每条弧的e[i]和l[i]找出e[i]=l[i]的关键活动。

算法实现

1输入顶点和弧信息建立其邻接表;计算每个顶点的入度

2对其进行拓扑排序排序过程中求顶点的ve[i]将得到的拓扑序列进栈

3按逆拓扑序列求顶点的vl[i]。计算每条弧的e[i]和l[i]找出e[i]=l[i]的关键活动。

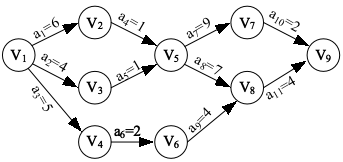
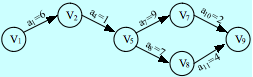
例如根据给定的右图求该AOE-网的关键活动及关键路径。

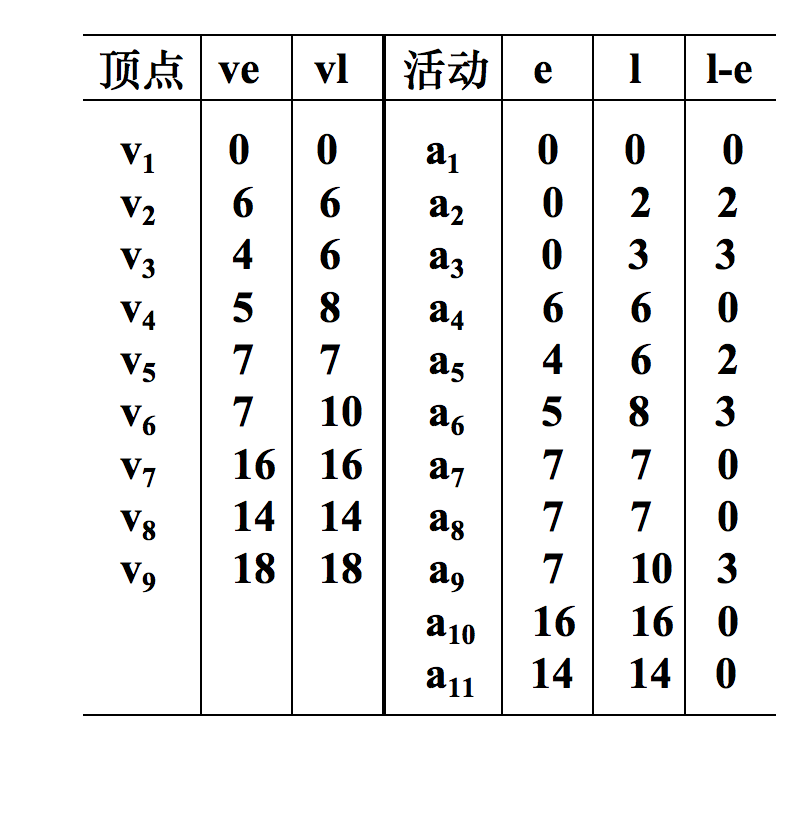
关键活动是a1, a4, a7, a8, a10, a11

它们构成了两条关键路径(v1v2v5v7v9)和(v1v2v5v8v9)

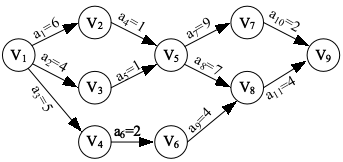
求出来的关键路径的图如下

说明

关键活动的速度提高是有限度的。
任何一项活动持续时间的改变都会影响关键路径的改变只有在不改变网的关键路径的情况下提高关键活动的速度才有效。若网中有几条关键路径单提高一条关键路径上的关键活动的速度是不能导致整个工程缩短工期。 必须同时提高在几条关键路径上的活动的速度。

三、关键路径求解过程演示

ppt上面很详细

https://download.csdn.net/download/u014206695/10767188

原文出处https://www.cnblogs.com/tojian/p/9914075.html