关于对回溯法解决组合问题的优化的理解

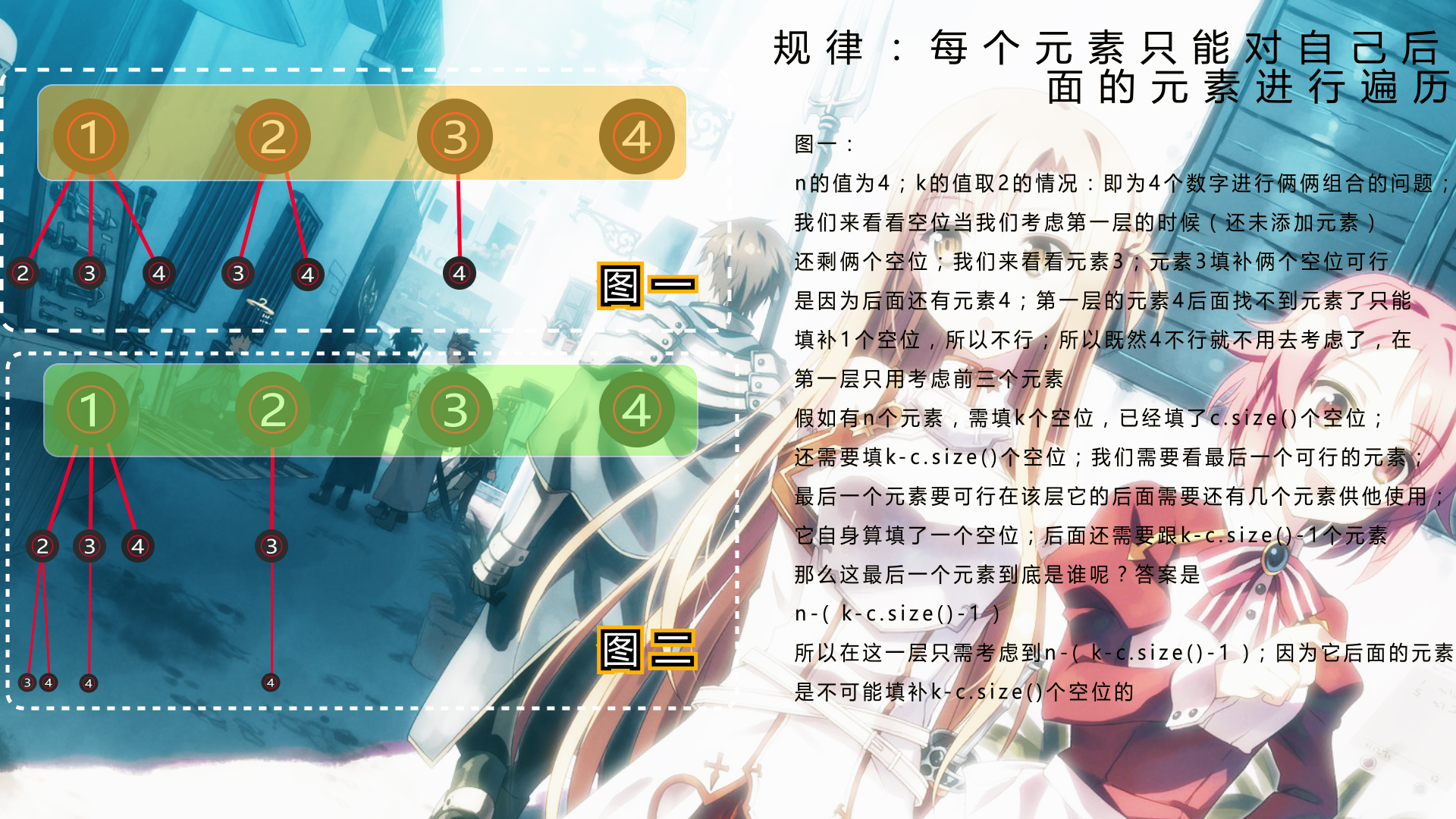
规律：每个元素只能对自己后面的元素进行遍历

图一：
n的值为4；k的值取2的情况：即为4个数字进行俩俩组合的问题；
我们来看看空位当我们考虑第一层的时候（还未添加元素）
还剩俩个空位；我们来看看元素3；元素3填补俩个空位可行
是因为后面还有元素4；第一层的元素4后面找不到元素了只能
填补1个空位，所以不行；所以既然4不行就不用去考虑了，在
第一层只用考虑前三个元素
假如有n个元素，需填k个空位，已经填了c.size()个空位；
还需要填k-c.size()个空位；我们需要看最后一个可行的元素；
最后一个元素要可行在该层它的后面需要还有几个元素供他使用；
它自身算填了一个空位；后面还需要跟k-c.size()-1个元素
那么这最后一个元素到底是谁呢？答案是
n-( k-c.size()-1 )
所以在这一层只需考虑到n-( k-c.size()-1 )；因为它后面的元素
是不可能填补k-c.size()个空位的
所以对于图一来说；第一层元素3为最后一个可行的元素；只要考虑到元素3

在图二中第一层元素2为最后一个可行的元素；
因为是递归所以第一层的规律对第二层同样适用，
第一层元素1下面的元素2,3,4（第二层）适用规律
第一层元素2下面的元素3（第二层）适用规律

以上可能说得不够好先说声抱歉啊，哈哈哈......