目录
- 前言
- cuda-gdb
- 未优化并行规约
- 优化后并行规约
- 结果分析
- 最后
前言
- 之前CUDA编程(四): CPU与GPU的矩阵乘法对比也看到了, 并行方面GPU真的是无往不利, 现在再看下第二个例子, 并行规约. 通过这次的例子会发现, 需要了解GPU架构, 然后写出与之对应的算法的, 两者结合才能得到令人惊叹的结果.
- 这次也会简要介绍下cuda-gdb的用法, 其实和gdb用法几乎一样, 也就是多了个cuda命令.
cuda-gdb
如果之前没有用过gdb, 可以速学一下, 就几个指令.
想要用cuda-gdb对程序进行调试, 首先你要确保你的gpu没有在运行操作系统界面, 比方说, 我用的是ubuntu, 我就需要用sudo service lightdm stop关闭图形界面, 进入tty1这种字符界面.
当然用ssh远程访问也是可以的.
接下来, 使用第二篇中矩阵加法的例子. 但是注意, 编译的使用需要改变一下, 加入**-g -G**参数, 其实和gdb是相似的.
nvcc -g -G CUDAAdd.cu -o CUDAAdd.o
然后使用
cuda-gdb CUDAAdd.o即可对程序进行调试.
在调试之前, 我把代码贴出来:
#include <stdio.h>
__global__ void add(float * x, float *y, float * z, int n){
int index = threadIdx.x + blockIdx.x * blockDim.x;
int stride = blockDim.x * gridDim.x;
for (int i = index; i < n; i += stride){
z[i] = x[i] + y[i];
}
}
int main()
{
int N = 1 << 20;
int nBytes = N * sizeof(float);
float *x, *y, *z;
cudaMallocManaged((void**)&x, nBytes);
cudaMallocManaged((void**)&y, nBytes);
cudaMallocManaged((void**)&z, nBytes);
for (int i = 0; i < N; ++i)
{
x[i] = 10.0;
y[i] = 20.0;
}
dim3 blockSize(256);
// 4096
dim3 gridSize((N + blockSize.x - 1) / blockSize.x);
add << < gridSize, blockSize >> >(x, y, z, N);
cudaDeviceSynchronize();
float maxError = 0.0;
for (int i = 0; i < N; i++){
maxError = fmax(maxError, (float)(fabs(z[i] - 30.0)));
}
printf ("max default: %.4f\n", maxError);
cudaFree(x);
cudaFree(y);
cudaFree(z);
return 0;
}
之后就是常规操作了, 添加断点, 运行, 下一步, 查看想看的数据. 不同点是cuda的指令, 例如
cuda block(1,0,0)可以从一开始block(0,0,0)切换到block(1,0,0).
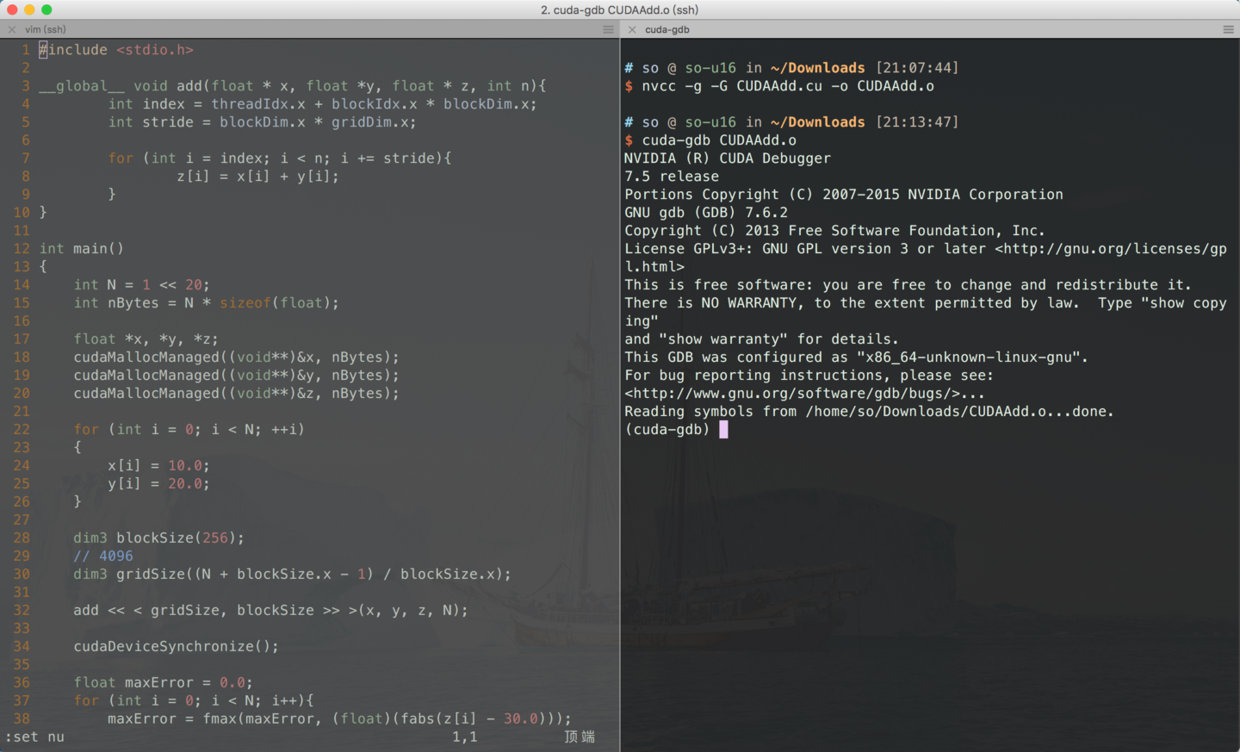
未优化并行规约
如果按照常规的思路, 两两进行进行加法运算. 每次步长翻倍即可, 从算法的角度来说, 这是没啥问题的. 但是没有依照GPU架构进行设计.
#include <stdio.h>
const int threadsPerBlock = 512;
const int N = 2048;
const int blocksPerGrid = (N + threadsPerBlock - 1) / threadsPerBlock; /* 4 */
__global__ void ReductionSum( float * d_a, float * d_partial_sum )
{
/* 申请共享内存, 存在于每个block中 */
__shared__ float partialSum[threadsPerBlock];
/* 确定索引 */
int i = threadIdx.x + blockIdx.x * blockDim.x;
int tid = threadIdx.x;
/* 传global memory数据到shared memory */
partialSum[tid] = d_a[i];
/* 传输同步 */
__syncthreads();
/* 在共享存储器中进行规约 */
for ( int stride = 1; stride < blockDim.x; stride *= 2 )
{
if ( tid % (2 * stride) == 0 )
partialSum[tid] += partialSum[tid + stride];
__syncthreads();
}
/* 将当前block的计算结果写回输出数组 */
if ( tid == 0 )
d_partial_sum[blockIdx.x] = partialSum[0];
}
int main()
{
int size = sizeof(float);
/* 分配显存空间 */
float * d_a;
float * d_partial_sum;
cudaMallocManaged( (void * *) &d_a, N * size );
cudaMallocManaged( (void * *) &d_partial_sum, blocksPerGrid * size );
for ( int i = 0; i < N; ++i )
d_a[i] = i;
/* 调用内核函数 */
ReductionSum << < blocksPerGrid, threadsPerBlock >> > (d_a, d_partial_sum);
cudaDeviceSynchronize();
/* 将部分和求和 */
int sum = 0;
for ( int i = 0; i < blocksPerGrid; ++i )
sum += d_partial_sum[i];
printf( "sum = %d\n", sum );
/* 释放显存空间 */
cudaFree( d_a );
cudaFree( d_partial_sum );
return(0);
}
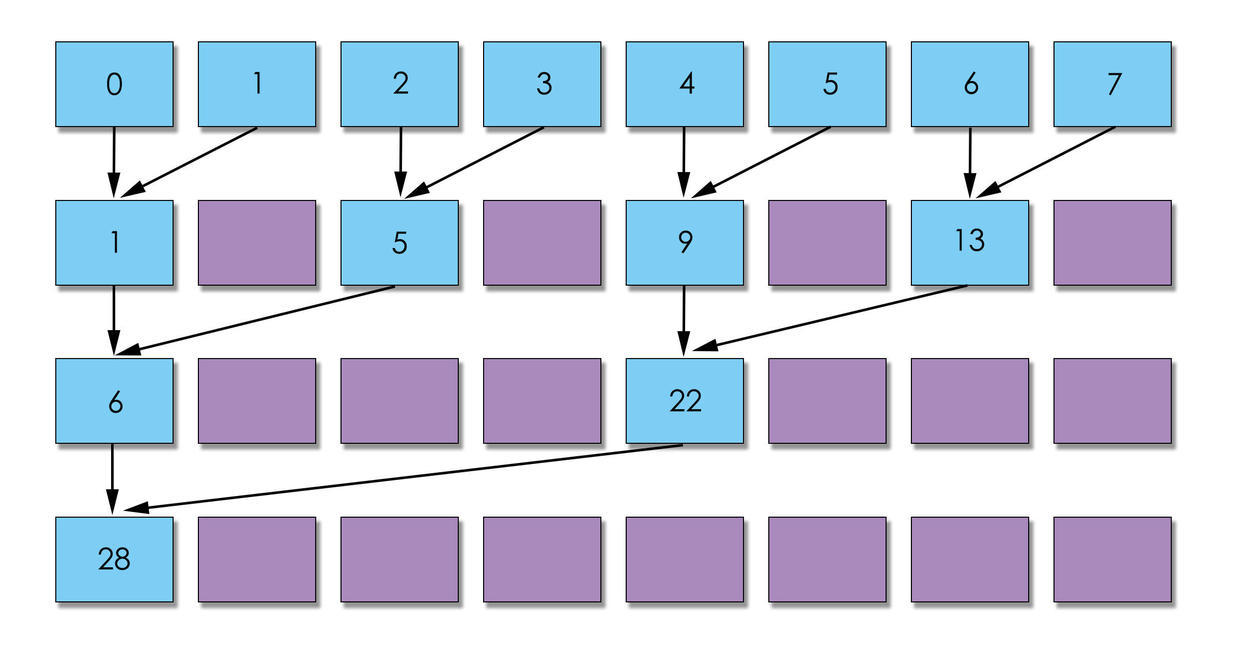
优化后并行规约
其实需要改动的地方非常小, 改变步长即可.
__global__ void ReductionSum( float * d_a, float * d_partial_sum )
{
// 相同, 略去
/* 在共享存储器中进行规约 */
for ( int stride = blockDim.x / 2; stride > 0; stride /= 2 )
{
if ( tid < stride )
partialSum[tid] += partialSum[tid + stride];
__syncthreads();
}
// 相同, 略去
}
结果分析
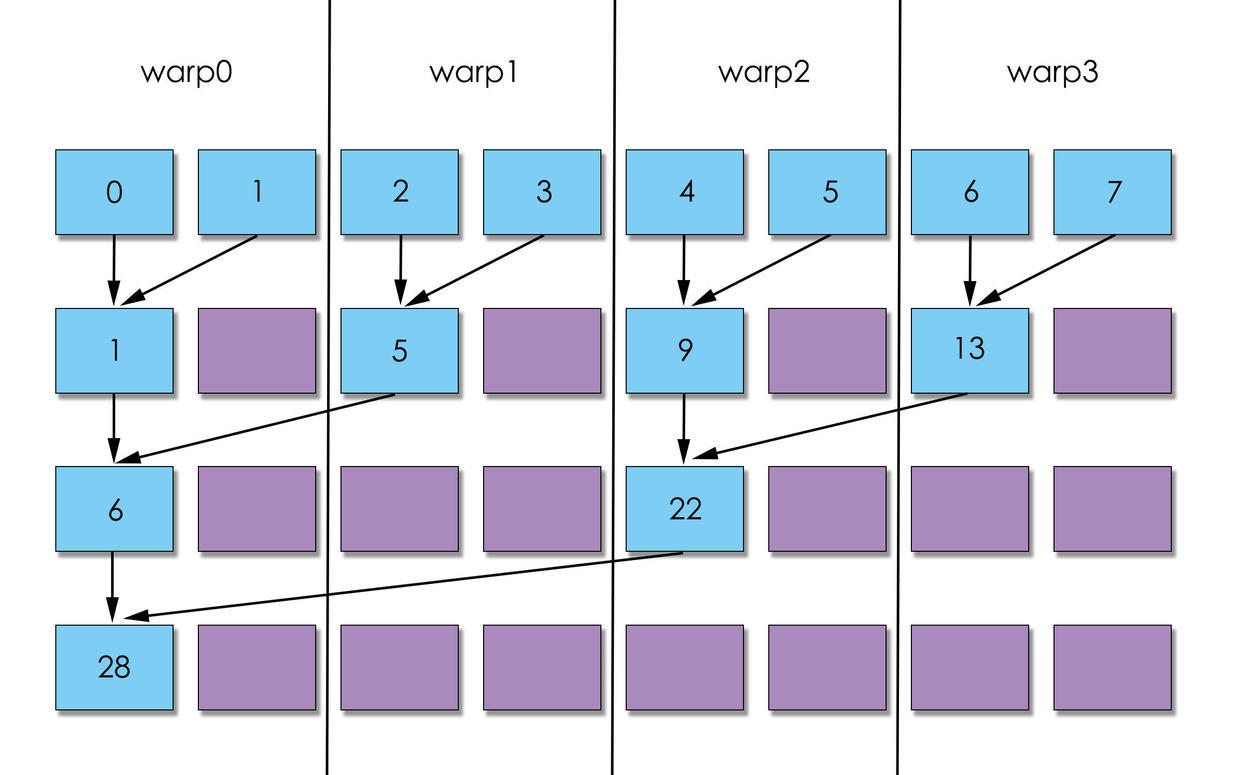
之前的文章里面也说过warp.
warp: GPU执行程序时的调度单位, 目前cuda的warp的大小为32, 同在一个warp的线程, 以不同数据资源执行相同的指令, 这就是所谓SIMT.
说人话就是, 这32个线程必须要干相同的事情, 如果有线程动作不一致, 就需要等待一波线程完成自己的工作, 然后再去做另外一件事情.
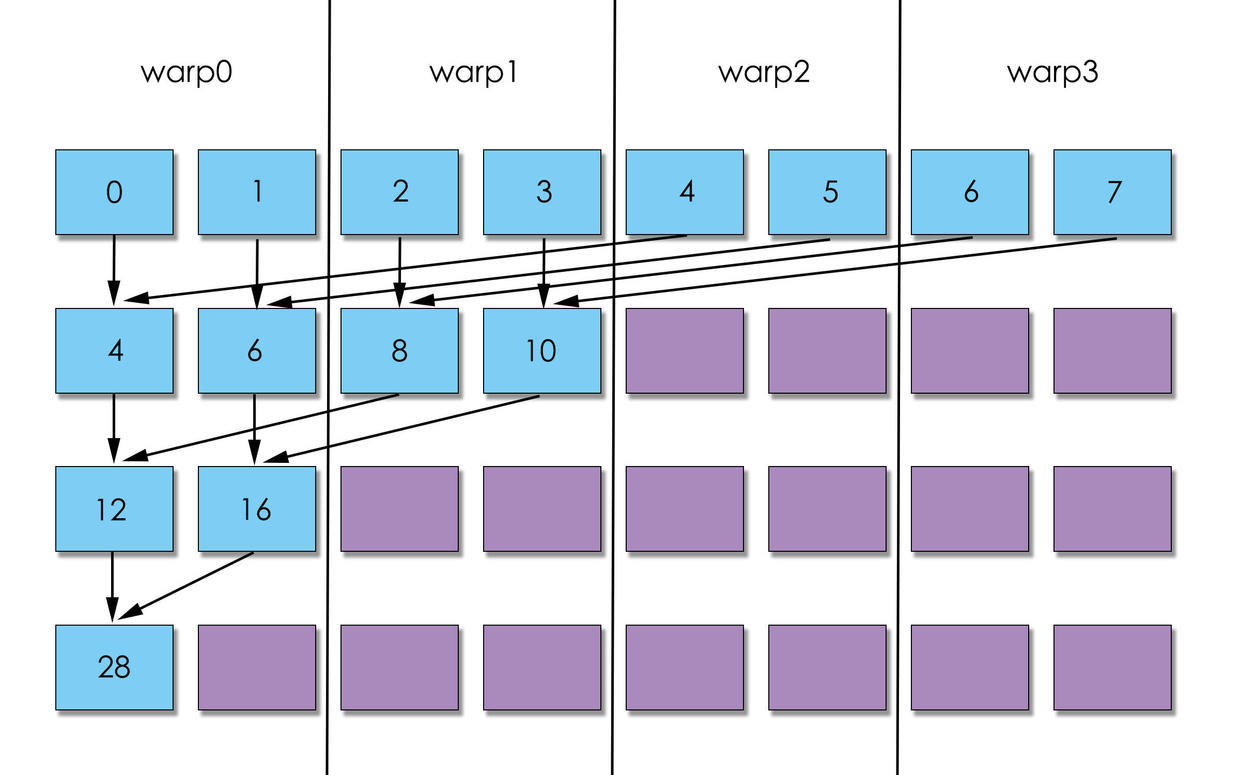
所以, 用图说话就是, 第二种方案可以更快将warp闲置, 交给GPU调度, 所以, 肯定是第二种更快.
图一在运算依次之后, 没有warp可以空闲, 而图二直接空闲2个warp. 图一到了第二次可以空闲2个warp, 而图二已经空闲3个warp. 我这副图只是示意图, 如果是实际的, 差距会更大.
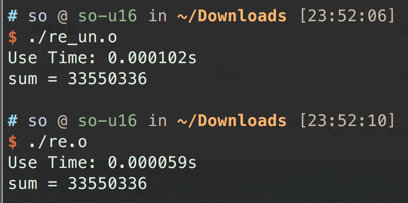
所以来看下运行耗时, 会发现差距还是很大的, 几乎是差了一倍. 不过GPU确实算力太猛, 这样看还不太明显, 有意放大数据量会更加明显.
最后
所以GPU又一次展示了强大的算力, 而且, 这次也看到了只是小小变动, 让算法更贴合架构, 就让运算耗时减半, 所以在优化方面可以做的工作真的是太多了, 之后还有更多优化相关的文章, 有意见或者建议, 评论区见哦~
共同学习,写下你的评论
评论加载中...
作者其他优质文章