unfortunately, no one can be told what the matrix is. you have to see it for yourself.
– morpheus
线性变换 linear transformation
通常 变换(transformation) 相当于函数(function)— f(x)f(x)f(x) ,给它一定的输入,它会产生相应的输出。在线性代数的场景中,变换(transformation)可以想象为输入某个向量,然后输出另一个向量的过程。
如果是这样,为什么使用变换(transformation)这个词,而不直接使用函数(function)呢?因为变换有移动的含义在里面,而更好的理解输入向量到输出向量的过程的方式是移动向量。
如果一个变换(transformation)接收一个输入向量,并输出一个新的向量,我们可以想象它是从输入的向量 (vector)移动到了输出的向量(vector)。然后我们把这种变换当做一个整体来理解,想象整个平面内任何向量(vectors)都随着这个变换(transformation)发生了各自的移动,等同于平面内所有的点随着该变换(transformation)移动到了另一个点。
而线性代数中的线性变换(linear transformation)是一种更易理解的、特殊的变换,它具备两个的条件:
- 向量在变换后仍然是直线,不会被扭曲;
- 原点不会发生移动。
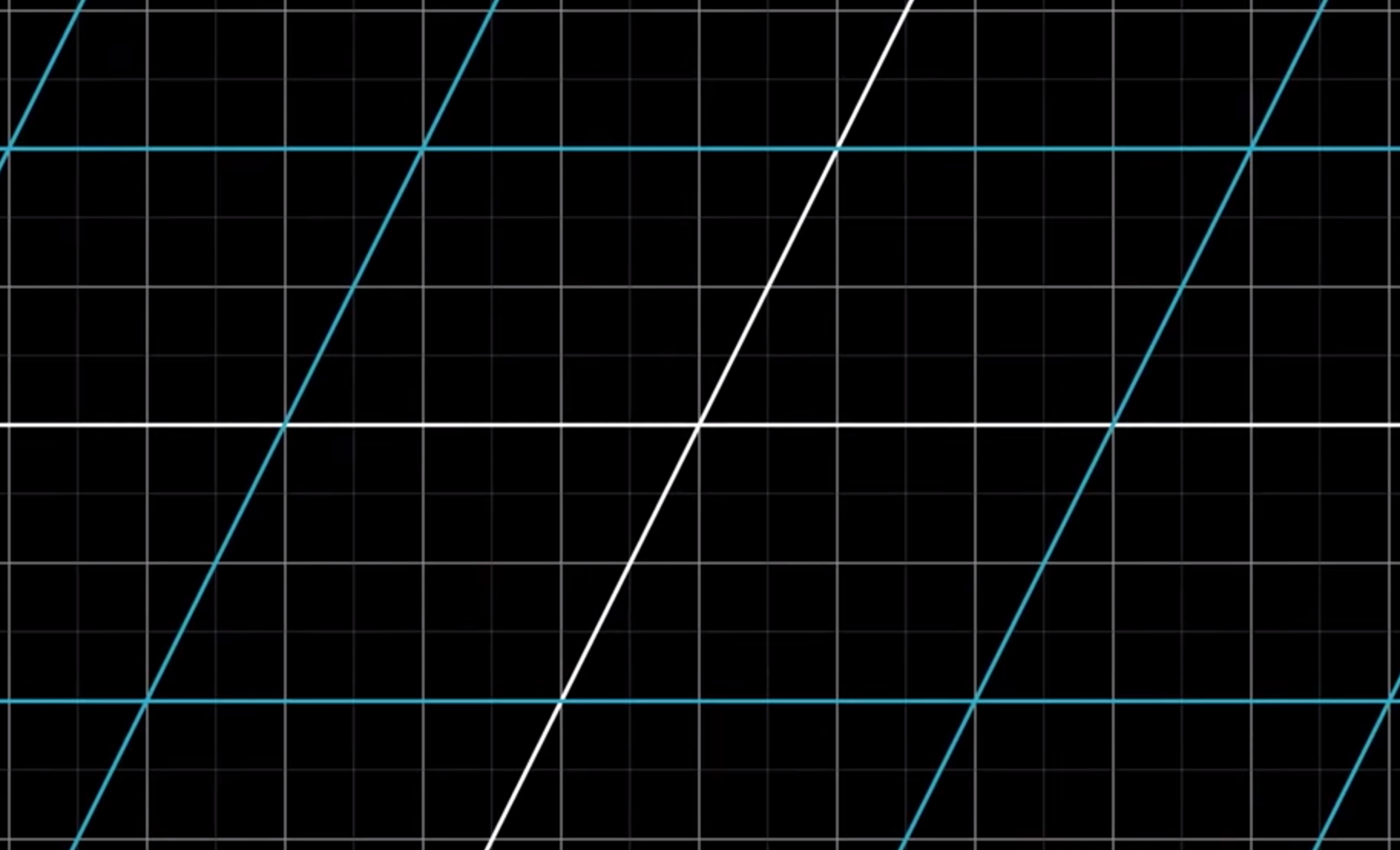
把一个平面想象为彼此间均匀且平行的网格,**线性变换会让网格中的线条依然保持平行且均匀。**例如下图是细实线组成的空间变换到粗实线组成的空间后的样子:
理解了线性变换后,我们如何用数学的方式来表示它呢?这样我们就可以把这个“公式”制作成计算机程序,然后输入一个向量的坐标,它就会给我们返回变换后的向量的坐标。
由于格式显示异常,文章后续部分请查看原文链接
共同学习,写下你的评论
评论加载中...
作者其他优质文章