SVD算法
奇异值分解(Singular Value Decompositionm,简称SVD)是在机器学习领域应用较为广泛的算法之一,也是学习机器学习算法绕不开的基石之一。SVD算法主要用在降维算法中的特征分解 、推荐系统 、自然语言处理 计算机视觉 等领域。奇异值分解(SVD)通俗一点讲就是将一个线性变换分解为两个线性变换,一个线性变换代表旋转,一个线性变换代表拉伸。
注:SVD是将一个矩阵分解成两个正交矩阵和一个对角矩阵,我们知道正交矩阵对应的变换是旋转变换,对角矩阵对应的变换是伸缩变换。
1.矩阵相关概念
上一篇:降维——PCA降维及原理推导 详细介绍了PCA算法,其中核心思想就是矩阵中的特征值和特征向量,为了后续内容的进行,在此,对此部分内容进一步做详细介绍。
1.1特征值和特征向量
关于特征值和特征向量的定义如下:A x = λ x Ax=\lambda x A x = λ x A ∈ R n × n A\in R^{n \times n} A ∈ R n × n x x x n n n x ∈ R n x \in R^n x ∈ R n λ \lambda λ A A A x x x λ \lambda λ
1.2特征分解
如果我们求出了矩阵A A A n n n λ 1 ≤ λ 2 ≤ ⋯ ≤ λ n λ_1≤λ_2≤\cdots≤λ_n λ 1 ≤ λ 2 ≤ ⋯ ≤ λ n n n n { w 1 , w 2 , ⋯ , w n } \{w_1,w_2,\cdots,w_n\} { w 1 , w 2 , ⋯ , w n } n n n A A A A = W Σ W − 1 A=W\Sigma W^{-1} A = W Σ W − 1 W = ( w 1 , w 2 , ⋯ , w n ) W=(w_1,w_2,\cdots,w_n) W = ( w 1 , w 2 , ⋯ , w n ) Σ \Sigma Σ Σ = ( λ 1 λ 2 ⋯ λ n ) \Sigma=\begin{pmatrix}\lambda_1&\\
&\lambda_2\\
&&\cdots\\
&&&\lambda_n
\end{pmatrix} Σ = ⎝ ⎜ ⎜ ⎛ λ 1 λ 2 ⋯ λ n ⎠ ⎟ ⎟ ⎞ W W W n n n ∣ ∣ w i ∣ ∣ 2 = 1 ||w_i||_2=1 ∣ ∣ w i ∣ ∣ 2 = 1 w i T w i = 1 w_i^Tw_i =1 w i T w i = 1 W W W n n n W T W = I W^TW=I W T W = I W T = W − 1 W^T=W^{-1} W T = W − 1 W W W A = W Σ W T A=W \Sigma W^T A = W Σ W T n × m n\times m n × m
2.特征分解的几何意义。
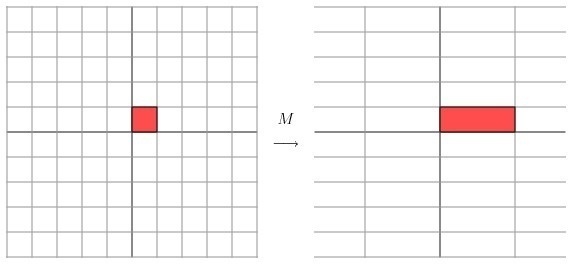
首先,要明确的是,一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵:M = [ 3 0 0 1 ] M=\begin{bmatrix}
3&0\\
0&1\\
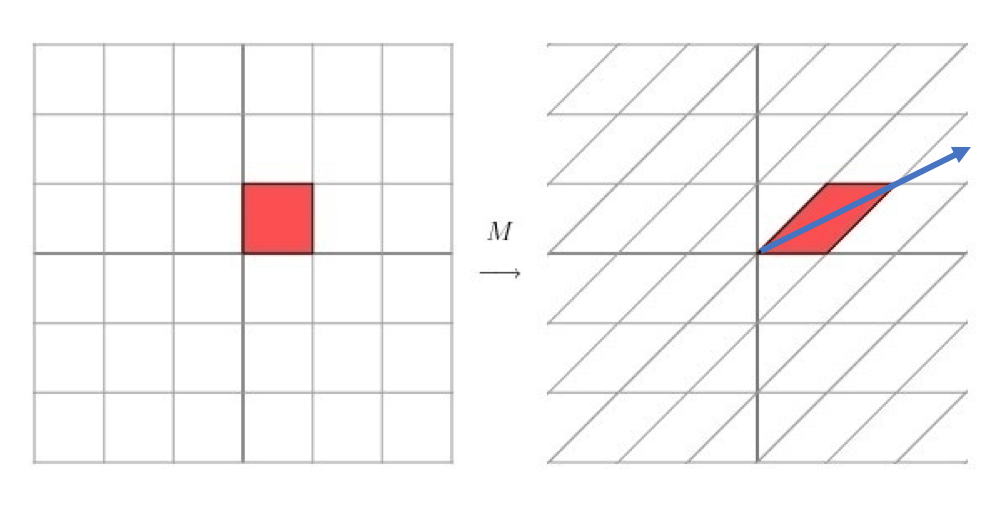
\end{bmatrix} M = [ 3 0 0 1 ] M M M ( x , y ) (x,y) ( x , y ) [ 3 0 0 1 ] [ x y ] = [ 3 x y ] \begin{bmatrix}
3&0\\
0&1
\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}3x\\y\end{bmatrix} [ 3 0 0 1 ] [ x y ] = [ 3 x y ] x x x y y y M = [ 1 1 0 1 ] M=\begin{bmatrix} 1&1 \\ 0&1 \end{bmatrix} M = [ 1 0 1 1 ] 如果我们想要描述好一个变换,那我们就描述好这个变换主要的变化方向就好了 。反过头来看看之前特征值分解的式子,分解得到的Σ矩阵是一个对角阵,里面的特征值是由大到小排列的,这些特征值所对应的特征向量就是描述这个矩阵变化方向(从主要的变化到次要的变化排列)。提取这个矩阵最重要的特征 。总结一下,特征值分解可以得到特征值与特征向量,特征值表示的是这个特征到底有多重要,而特征向量表示这个特征是什么,可以将每一个特征向量理解为一个线性的子空间,我们可以利用这些线性的子空间干很多的事情。不过,特征值分解也有很多的局限,比如说变换的矩阵必须是方阵 。
3.奇异值分解
正如上文所示,特征分解只适用于方阵的情况,但是对于不是方阵的矩阵,我们需要用SVD算法进行特征分解。假设我们定义矩阵A A A A = U Σ V T A = U\Sigma V^T A = U Σ V T U U U m × m m \times m m × m Σ \Sigma Σ m × n m\times n m × n V V V n × n n\times n n × n U U U V V V U T U = I , V T V = I U^TU=I,V^TV=I U T U = I , V T V = I r r r A A A A = ( U 1 U 2 ) ⎵ U ( Σ 1 0 r × ( n − r ) 0 ( m − n ) × r 0 ( m − r ) × ( n − r ) ) ⎵ Σ ( V 1 T V 2 T ) ⎵ V T = U Σ V T = U 1 Σ 1 V 1 T = Σ i = 1 r σ i u i V i T \begin{aligned}A&=\underbrace{(U_1\ U_2)}_{U}\ \underbrace{\begin{pmatrix}\Sigma_1&0_{r\times(n-r)}\\
0_{(m-n)\times r}&0_{(m-r)\times(n-r)}
\end{pmatrix}}_{\Sigma}\ \underbrace{\begin{pmatrix}V_1^T\\V_2^T\end{pmatrix}}_{V^T}\\
&=U\Sigma V^T\\
&=U_1\Sigma_1V_1^T\\
&=\Sigma_{i=1}^r\sigma_iu_iV_i^T
\end{aligned} A = U ( U 1 U 2 ) Σ ( Σ 1 0 ( m − n ) × r 0 r × ( n − r ) 0 ( m − r ) × ( n − r ) ) V T ( V 1 T V 2 T ) = U Σ V T = U 1 Σ 1 V 1 T = Σ i = 1 r σ i u i V i T U , Σ , V U,\Sigma,V U , Σ , V ( A T A ) v i = λ i v i (A^TA)v_i=\lambda_iv_i ( A T A ) v i = λ i v i A T A ∈ R n × n A^TA \in R^{n \times n} A T A ∈ R n × n n n n n n n v i v_i v i 按行排列 ,就构成了SVD公式中的V矩阵了。A A T ∈ R m × m AA^T \in R^{m\times m} A A T ∈ R m × m ( A A T ) u i = λ 1 u i (AA^T)u_i=\lambda_1u_i ( A A T ) u i = λ 1 u i A A T AA^T A A T m m m m m m u i u_i u i A A T AA^T A A T 按列排列 就构成了m × m m\times m m × m U U U U U U
证明:为什么A T A A^TA A T A A A T AA^T A A T A = U Σ V T A T = V Σ T U T A=U\Sigma V^T\qquad\qquad\qquad A^T=V\Sigma^TU^T A = U Σ V T A T = V Σ T U T A T A = V Σ T U T U Σ V T = V Σ 2 V T ⋯ ( 1 ) A^TA=V\Sigma^TU^TU\Sigma V^T=V\Sigma^2V^T \qquad\qquad \cdots(1) A T A = V Σ T U T U Σ V T = V Σ 2 V T ⋯ ( 1 ) U T U = I , Σ T Σ = Σ 2 U^TU=I,\Sigma^T\Sigma=\Sigma^2 U T U = I , Σ T Σ = Σ 2
得到奇异向量以后,我们接着求奇异值,求奇异值的方法有两种:U ∈ M n ( R ) U \in M_n(R) U ∈ M n ( R ) U T U = I U^TU=I U T U = I U U U
第一种A = U Σ V T ⇒ A V = U Σ V T V ⇒ A V = U Σ ⇒ A v i = σ i u i A=U\Sigma V^T \Rightarrow AV=U\Sigma V^TV \Rightarrow AV=U\Sigma \Rightarrow Av_i=\sigma_iu_i A = U Σ V T ⇒ A V = U Σ V T V ⇒ A V = U Σ ⇒ A v i = σ i u i σ i = A v i u i \sigma_i=\frac{Av_i}{u_i} σ i = u i A v i
第二种A T A A^TA A T A A A T AA^T A A T σ i = λ i \sigma_i=\sqrt{\lambda_i} σ i = λ i σ i \sigma_i σ i σ i \sigma_i σ i Σ \Sigma Σ
4.SVD算法示例
假定矩阵A A A A = ( 0 1 1 1 1 0 ) \mathbf{A} = \left( \begin{array}{ccc} 0& 1\\ 1& 1\\ 1& 0 \end{array} \right) A = ⎝ ⎛ 0 1 1 1 1 0 ⎠ ⎞ A T A A^TA A T A A A T AA^T A A T A T A = ( 0 1 1 1 1 0 ) ( 0 1 1 1 1 0 ) = ( 2 1 1 2 ) \mathbf{A^TA} = \left( \begin{array}{ccc} 0& 1 &1\\ 1&1& 0 \end{array} \right) \left( \begin{array}{ccc} 0& 1\\ 1& 1\\ 1& 0 \end{array} \right) = \left( \begin{array}{ccc} 2& 1 \\ 1& 2 \end{array} \right) A T A = ( 0 1 1 1 1 0 ) ⎝ ⎛ 0 1 1 1 1 0 ⎠ ⎞ = ( 2 1 1 2 ) A A T = ( 0 1 1 1 1 0 ) ( 0 1 1 1 1 0 ) = ( 1 1 0 1 2 1 0 1 1 ) \mathbf{AA^T} = \left( \begin{array}{ccc} 0& 1\\ 1& 1\\ 1& 0 \end{array} \right) \left( \begin{array}{ccc} 0& 1 &1\\ 1&1& 0 \end{array} \right) = \left( \begin{array}{ccc} 1& 1 & 0\\ 1& 2 & 1\\ 0& 1& 1 \end{array} \right) A A T = ⎝ ⎛ 0 1 1 1 1 0 ⎠ ⎞ ( 0 1 1 1 1 0 ) = ⎝ ⎛ 1 1 0 1 2 1 0 1 1 ⎠ ⎞ A T A A^TA A T A λ 1 = 3 ; v 1 = ( 1 / 2 1 / 2 ) ; λ 2 = 1 ; v 2 = ( − 1 / 2 1 / 2 ) \lambda_1= 3; v_1 = \left( \begin{array}{ccc} 1/\sqrt{2} \\ 1/\sqrt{2} \end{array} \right); \lambda_2= 1; v_2 = \left( \begin{array}{ccc} -1/\sqrt{2} \\ 1/\sqrt{2} \end{array} \right) λ 1 = 3 ; v 1 = ( 1 / 2 1 / 2 ) ; λ 2 = 1 ; v 2 = ( − 1 / 2 1 / 2 ) A A T AA^T A A T λ 1 = 3 ; u 1 = ( 1 / 6 2 / 6 1 / 6 ) ; λ 2 = 1 ; u 2 = ( 1 / 2 0 − 1 / 2 ) ; λ 3 = 0 ; u 3 = ( 1 / 3 − 1 / 3 1 / 3 ) \lambda_1= 3; u_1 = \left( \begin{array}{ccc} 1/\sqrt{6} \\ 2/\sqrt{6} \\ 1/\sqrt{6} \end{array} \right); \lambda_2= 1; u_2 = \left( \begin{array}{ccc} 1/\sqrt{2} \\ 0 \\ -1/\sqrt{2} \end{array} \right); \lambda_3= 0; u_3 = \left( \begin{array}{ccc} 1/\sqrt{3} \\ -1/\sqrt{3} \\ 1/\sqrt{3} \end{array} \right) λ 1 = 3 ; u 1 = ⎝ ⎛ 1 / 6 2 / 6 1 / 6 ⎠ ⎞ ; λ 2 = 1 ; u 2 = ⎝ ⎛ 1 / 2 0 − 1 / 2 ⎠ ⎞ ; λ 3 = 0 ; u 3 = ⎝ ⎛ 1 / 3 − 1 / 3 1 / 3 ⎠ ⎞ A v i = σ i u i , i = 1 , 2 Av_i=\sigma_i u_i,i=1,2 A v i = σ i u i , i = 1 , 2 ( 0 1 1 1 1 0 ) ( 1 / 2 1 / 2 ) = σ 1 ( 1 / 6 2 / 6 1 / 6 ) ⇒ σ 1 = 3 \left( \begin{array}{ccc} 0& 1\\ 1& 1\\ 1& 0 \end{array} \right) \left( \begin{array}{ccc} 1/\sqrt{2} \\ 1/\sqrt{2} \end{array} \right) = \sigma_1 \left( \begin{array}{ccc} 1/\sqrt{6} \\ 2/\sqrt{6} \\ 1/\sqrt{6} \end{array} \right) \Rightarrow \sigma_1=\sqrt{3} ⎝ ⎛ 0 1 1 1 1 0 ⎠ ⎞ ( 1 / 2 1 / 2 ) = σ 1 ⎝ ⎛ 1 / 6 2 / 6 1 / 6 ⎠ ⎞ ⇒ σ 1 = 3 ( 0 1 1 1 1 0 ) ( − 1 / 2 1 / 2 ) = σ 2 ( 1 / 2 0 − 1 / 2 ) ⇒ σ 2 = 1 \left( \begin{array}{ccc} 0& 1\\ 1& 1\\ 1& 0 \end{array} \right) \left( \begin{array}{ccc} -1/\sqrt{2} \\ 1/\sqrt{2} \end{array} \right) = \sigma_2 \left( \begin{array}{ccc} 1/\sqrt{2} \\ 0 \\ -1/\sqrt{2} \end{array} \right) \Rightarrow \sigma_2=1 ⎝ ⎛ 0 1 1 1 1 0 ⎠ ⎞ ( − 1 / 2 1 / 2 ) = σ 2 ⎝ ⎛ 1 / 2 0 − 1 / 2 ⎠ ⎞ ⇒ σ 2 = 1 A = U Σ V T = ( 1 / 6 1 / 2 1 / 3 2 / 6 0 − 1 / 3 1 / 6 − 1 / 2 1 / 3 ) ( 3 0 0 1 0 0 ) ( 1 / 2 1 / 2 − 1 / 2 1 / 2 ) A=U\Sigma V^T = \left( \begin{array}{ccc} 1/\sqrt{6} & 1/\sqrt{2} & 1/\sqrt{3} \\ 2/\sqrt{6} & 0 & -1/\sqrt{3}\\ 1/\sqrt{6} & -1/\sqrt{2} & 1/\sqrt{3} \end{array} \right) \left( \begin{array}{ccc} \sqrt{3} & 0 \\ 0 & 1\\ 0 & 0 \end{array} \right) \left( \begin{array}{ccc} 1/\sqrt{2} & 1/\sqrt{2} \\ -1/\sqrt{2} & 1/\sqrt{2} \end{array} \right) A = U Σ V T = ⎝ ⎛ 1 / 6 2 / 6 1 / 6 1 / 2 0 − 1 / 2 1 / 3 − 1 / 3 1 / 3 ⎠ ⎞ ⎝ ⎛ 3 0 0 0 1 0 ⎠ ⎞ ( 1 / 2 − 1 / 2 1 / 2 1 / 2 )
5.奇异值分解特性
对于奇异值,它跟我们特征分解中的特征值类似,在奇异值矩阵中也是按照从大到小排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例 。也就是说,我们也可以用最大的k k k A m × n = U m × m Σ m × n V n × n T ≈ U m × k Σ k × k V k × n T A_{m \times n} = U_{m \times m}\Sigma_{m \times n} V^T_{n \times n} \approx U_{m \times k}\Sigma_{k \times k} V^T_{k \times n} A m × n = U m × m Σ m × n V n × n T ≈ U m × k Σ k × k V k × n T k k k n n n A A A U m × k , Σ k × k , V k × n T U_{m \times k},\Sigma_{k \times k} ,V^T_{k \times n} U m × k , Σ k × k , V k × n T 奇异值分解(SVD)原理与在降维中的应用
参考文献